सभी के बारे में बेयस प्रमेय क्या है?

Question

बेयस प्रमेय से संबंधित मुख्य विचार, यानी अवधारणाएं क्या हैं ? मैं जटिल गणितीय संकेतन की कोई व्युत्पत्ति नहीं माँग रहा हूँ।

Comments

संबं धत ल ं क आँकड़े

— शेन

मैं इस लिंक को किसी प्रकार के निम्न-स्तरीय-स्पष्टीकरण के रूप में भी सुझाना चाहता हूं: yudkowsky.net/rational/bayes

— steffen

बेयस प्रमेय दृश्य प्रतिनिधित्व के बिना एक मैला हो सकता है-जैसा कि अक्सर गणित में होता है। बायेसियन संभावनाओं के लिए प्रायिकता वर्ग या संभावना पेड़ों का उपयोग क्यों नहीं किया जाता है? जब नया डेटा आता है, तो यह नमूना स्थान में से कुछ को बंद कर देता है (जैसे कि किसी बीमारी के लिए सकारात्मक परीक्षण किया जा रहा है नकारात्मक परीक्षण किया जा रहा है)। तब नमूना स्थान केवल संभावनाओं का एक उप-समुच्चय बन जाता है, जिसका परीक्षण सकारात्मक हो सकता है, शायद- और कोई भी इस पर पूरी तरह से विचार करता है। मुझे जो कठिनाई है, वह असतत संभावनाओं के बजाय संभावना वितरण के लिए बे को लागू कर रही है। मैथ्स नारकीय भयानक है!

Answer 1

बेयस का प्रमेय संभावना सिद्धांत का एक अपेक्षाकृत सरल, लेकिन मौलिक परिणाम है जो कुछ सशर्त संभावनाओं की गणना के लिए अनुमति देता है। सशर्त सम्भावनाएँ केवल वे सम्भावनाएँ हैं जो किसी एक घटना के दूसरे की संभावना पर प्रभाव को दर्शाती हैं।

सीधे शब्दों में, अपने सबसे प्रसिद्ध रूप में, यह बताता है कि एक परिकल्पना की संभावना नए डेटा ( पी (एच। डी) ; जिसे पश्च संभावना कहा जाता है) निम्नलिखित समीकरण के बराबर है: देखे गए डेटा की संभावना परिकल्पना दी गई है। P (D | H) ; सशर्त संभाव्यता कहा जाता है), उस समय की संभावना नए सिद्धांत ( P (H) , H की पूर्व संभाव्यता कहा जाता है ) से पहले सच होने की संभावना, उस डेटा, अवधि को देखने की संभावना से विभाजित पी (डी ); डी की सीमांत संभावना कहा जाता है।

औपचारिक रूप से, समीकरण इस तरह दिखता है:

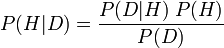
बेयस प्रमेय का महत्व काफी हद तक इसके उचित उपयोग के कारण संभावना पर विचार के स्कूलों के बीच विवाद का बिंदु है। एक व्यक्तिपरक बायेसियन के लिए (जो कि विश्वास की व्यक्तिपरक डिग्री होने के रूप में संभावना की व्याख्या करता है) बेयस प्रमेय सिद्धांत में परीक्षण, सिद्धांत चयन और अन्य प्रथाओं के लिए आधारशिला प्रदान करता है, समीकरण में उनके व्यक्तिपरक संभावना निर्णयों को प्लग करके और इसके साथ चल रहा है। एक निरंतरवादी के लिए (जो सापेक्ष आवृत्तियों को सीमित करने के रूप में संभाव्यता की व्याख्या करता है ), बेयस प्रमेय का यह उपयोग एक दुरुपयोग है, और वे इसके बजाय सार्थक (गैर-व्यक्तिपरक) पुजारियों का उपयोग करने का प्रयास करते हैं (जैसा कि संभाव्यता की अब तक व्याख्या के तहत उद्देश्य बायेसियन करते हैं)।

Comments

अच्छा उत्तर। मेरे पास एक छोटी सी वक्रोक्ति है: शब्द "व्यक्तिपरक" और "उद्देश्य" का उपयोग काफी उपयुक्त नहीं है, क्योंकि कोई भी तरीका "उद्देश्य" नहीं है। मैं कहता हूँ कि अधिकतावादी और "उद्देश्य" बायेसियन केवल कुछ नियमों या मानकों का उपयोग करके अपने संभाव्यता वितरण को प्राप्त करते हैं। इसलिए हाथ में विशिष्ट मामले के लिए tayloring करने के बजाय, एक लगातार / उद्देश्य बायेसियन "डिफ़ॉल्ट" विकल्प (इस प्रकार उनकी विषय-वस्तु को छिपाते हुए) लागू करेगा।

— probabilityislogic

यदि आप कुछ वास्तविक मूल्य (6 वर्ष की आयु के बच्चों की ऊंचाई कहते हैं) को माप रहे हैं, तो P (D) क्या है? क्या यह डेटा की पीडीएफ है? किस मामले में आप केवल पश्च बिंदु-वार की गणना करते हैं, जैसे: ? $P(x|H|D) = \frac{P(x|D|H)P(x|H)}{P(x|D)}$

— n

Answer 2

मुझे खेद है, लेकिन यहाँ कुछ भ्रम प्रतीत होता है: बेयस की प्रमेय, अनुपस्थित बायेसियन- फ़्रीक्वेंटिस्ट बहस की चर्चा के लिए नहीं है । यह एक प्रमेय है जो विचार के दोनों स्कूलों के अनुरूप है (यह कोलमोगोरोव की प्रायिकता स्वयंसिद्धों के अनुरूप है)।

बेशक, बेयस का प्रमेय बेयिसियन आँकड़ों का मूल है, लेकिन प्रमेय स्वयं सार्वभौमिक है। आवृत्तियों और बेयसियंस के बीच टकराव ज्यादातर इस बात से संबंधित है कि पूर्व वितरण को कैसे परिभाषित किया जा सकता है या नहीं।

तो, अगर सवाल बेयस प्रमेय के बारे में है (और बायेसियन आँकड़े नहीं):

बेयस की प्रमेय परिभाषित करती है कि कोई विशिष्ट सशर्त संभावनाओं की गणना कैसे कर सकता है। उदाहरण के लिए कल्पना कीजिए कि आप जानते हैं: किसी व्यक्ति के लक्षण ए होने की संभावना, यह देखते हुए कि उन्हें बीमारी है एक्स पी (ए | एक्स); सामान्य रूप से रोग एक्स पी (एक्स) में किसी की संभावना; सामान्य रूप से लक्षण पी (ए) वाले किसी व्यक्ति की संभावना। जानकारी के इन 3 टुकड़ों के साथ आप किसी व्यक्ति की बीमारी एक्स की संभावना की गणना कर सकते हैं, यह देखते हुए कि उनके पास सहानुभूति ए पी (एक्स | ए) है।

Comments

मैं आपके प्रारंभिक पैराग्राफ के साथ भाग लेने से असहमत हूं क्योंकि प्रश्न बेयस प्रमेय की अवधारणा के बारे में पूछते हैं। फ़्रीक्वेंटिस्ट-बायेसियन बहस प्रश्न के इस भाग के लिए प्रासंगिक है। कोलमोगोरोव स्वयंसिद्ध बेयस प्रमेय को वैचारिक महत्व नहीं देते हैं जैसा कि "विस्तारित तर्क के रूप में संभावना" स्वयंसिद्ध करते हैं।

— probabilityislogic

Answer 3

बेयस प्रमेय एक सशर्त प्रायिकता को दूसरी सशर्त प्रायिकता P ( B | A ) को घुमाने का एक तरीका है ।$P(A|B)$$P(B|A)$

$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

आप बेयस के प्रमेय को इस प्रकार समझ सकते हैं। सशर्त संभाव्यता की अनुपात परिभाषा से शुरू करें:

$P(B|A) = \frac{P(AB)}{P(A)}$

$P(AB)$$A$$B$$P(A)$$A$

$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

और हे प्रिस्टो:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

इस तरह से एक सशर्त संभावना को घुमाने के लिए बिंदु क्या है, इस संभावना का अनुमान लगाने के सामान्य उदाहरण पर विचार करें कि किसी को कोई बीमारी है जो उन्हें एक लक्षण है, अर्थात, हम जानते हैं कि उनके पास एक लक्षण है - हम बस कर सकते हैं इसे देखें - लेकिन हम निश्चित नहीं हो सकते हैं कि क्या उन्हें कोई बीमारी है और इसका पता लगाना है। मैं सूत्र के साथ शुरू करूँगा और वापस काम करूँगा।

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

तो इसे बाहर काम करने के लिए, आपको लक्षण की पूर्व संभाव्यता, रोग की पूर्व संभावना (अर्थात, लक्षण या बीमारी कितनी सामान्य या दुर्लभ है) जानने की आवश्यकता है और यह भी संभावना है कि किसी के पास कोई लक्षण है जिसे हम जानते हैं कि कोई व्यक्ति है एक बीमारी (जैसे, महंगी समय लेने वाली लैब परीक्षणों के माध्यम से)।

यह इससे कहीं अधिक जटिल हो सकता है, उदाहरण के लिए, यदि आपके पास कई रोग और लक्षण हैं, लेकिन विचार समान है। और भी आम तौर पर, बेयस प्रमेय अक्सर एक उपस्थिति बनाता है यदि आपके पास कारणों (जैसे, रोग) और प्रभाव (जैसे, लक्षण) के बीच संबंधों की संभावना सिद्धांत है और आपको पीछे की ओर तर्क करने की आवश्यकता है (उदाहरण के लिए, आपको कुछ लक्षण दिखाई देते हैं जिनसे आप चाहते हैं अंतर्निहित बीमारी का पता लगाने के लिए)।

Answer 4

विचार के दो मुख्य स्कूल हैं सांख्यिकी: लगातारवादी और बायेसियन ।

बेयस प्रमेय को उत्तरार्द्ध के साथ करना है और इसे समझने के तरीके के रूप में देखा जा सकता है कि एक सिद्धांत के सत्य होने की संभावना नए साक्ष्य के प्रभाव से कैसे प्रभावित होती है। इसे सशर्त संभाव्यता के रूप में जाना जाता है। आप गणित को संभालने के लिए इसे देखना चाह सकते हैं ।

Answer 5

मैं आपको एक बहुत ही सहज ज्ञान युक्त अंतर्दृष्टि देता हूं। मान लीजिए आप 10 बार एक सिक्का उछाल रहे हैं और आपको 8 सिर और 2 पूंछ मिलते हैं। आपके दिमाग में यह सवाल आएगा कि क्या यह सिक्का सिर के पक्षपाती है या नहीं।

अब यदि आप पारंपरिक परिभाषाओं या संभावना के लगातार दृष्टिकोण से जाते हैं, तो आप कह सकते हैं कि सिक्का निष्पक्ष है और यह एक असाधारण घटना है। इसलिए आप निष्कर्ष निकालेंगे कि टॉस के बाद एक सिर पाने की संभावना भी 50% है।

लेकिन मान लीजिए आप बायेसियन हैं। आप वास्तव में सोचेंगे कि जब से आपको असाधारण रूप से उच्च संख्या में सिर मिले हैं, सिक्के का सिर की तरफ एक पूर्वाग्रह है। इस संभावित पूर्वाग्रह की गणना करने के तरीके हैं। आप उनकी गणना करेंगे और फिर जब आप अगली बार सिक्का उछालेंगे, तो आप निश्चित रूप से एक हेड कहेंगे।

तो, बायेसियन संभावना इस विश्वास के बारे में है कि आप अपने द्वारा देखे गए डेटा के आधार पर विकसित होते हैं। मुझे उम्मीद है कि यह काफी सरल था।

Comments

बेशक, सिर्फ़ नतीजे की तुलना में एक सिक्का टॉस में अधिक डेटा होता है - एक समझदार बायेसियन अभी भी शायद दांव लगाएगा, क्योंकि पिछले डेटा के वजन के कारण, और क्योंकि सिक्का और सिक्का फ्लिप निष्पक्ष दिखता है। जब तक, शायद, आप सिक्का नहीं देख सकते हैं, या सिक्का फ़्लिप किया जा रहा है। जिस स्थिति में आप यह भी नहीं जानते हैं कि डेटा के साथ शुरू करने के लिए जाली नहीं है, और आप अपने

— पुजारियों

Answer 6

बेयस की प्रमेय दो विचारों से संबंधित है: संभावना और संभावना। संभावना कहती है: इस मॉडल को देखते हुए, ये परिणाम हैं। तो: एक उचित सिक्का दिया, मैं समय का 50% सिर मिल जाएगा। संभावना कहती है: इन परिणामों को देखते हुए, यह हम मॉडल के बारे में कह सकते हैं। तो: यदि आप 100 बार एक सिक्का उछालते हैं और 88 सिर प्राप्त करते हैं (पिछले उदाहरण पर लेने और इसे और अधिक चरम बनाने के लिए), तो संभावना है कि उचित सिक्का मॉडल सही नहीं है।

बेयस के प्रमेय का वर्णन करने के लिए उपयोग किए जाने वाले मानक उदाहरणों में से एक रोग के लिए परीक्षण का विचार है: यदि आप एक परीक्षण लेते हैं जो 95% एक बीमारी के लिए सटीक है, जो कि आबादी के 10000 में से 1 है, और आप सकारात्मक परीक्षण करते हैं, क्या संभावनाएं हैं कि आपको बीमारी है?

अनुभवहीन उत्तर 95% है, लेकिन यह इस मुद्दे की अनदेखी करता है कि 10000 लोगों में से 9999 पर 5% परीक्षण एक झूठी सकारात्मक देगा। तो बीमारी होने की आपकी संभावना 95% से कम है।

अस्पष्ट वाक्यांश "क्या संभावनाएं हैं" का मेरा उपयोग जानबूझकर किया गया है। संभाव्यता / संभावना भाषा का उपयोग करने के लिए: परीक्षण की सटीक संभावना 95% है, लेकिन आप जो जानना चाहते हैं वह संभावना है कि आपको बीमारी है।

थोड़ा दूर विषय: अन्य क्लासिक उदाहरण जो बेयस प्रमेय का उपयोग सभी पाठ्यपुस्तकों में हल करने के लिए किया जाता है वह मोंटी हॉल समस्या है: आप एक क्विज़ शो पर हैं। तीन दरवाजों में से एक के पीछे एक पुरस्कार है। आप दरवाजा एक का चयन करें। मेजबान कोई पुरस्कार प्रकट करने के लिए दरवाजा तीन खोलता है। क्या आपको मौका देखते हुए डोर टू में बदलाव करना चाहिए?

मुझे प्रश्न का पुनर्लेखन पसंद है (नीचे संदर्भ का सौजन्य): आप एक क्विज़ शो पर हैं। एक लाख दरवाजे के पीछे एक पुरस्कार है। आप दरवाजा एक का चयन करें। मेजबान कोई पुरस्कार प्रकट करने के लिए दरवाजे 104632 को छोड़कर अन्य सभी दरवाजे खोल देता है। क्या आपको दरवाजा 104632 में बदलना चाहिए?

मेरी पसंदीदा पुस्तक जो बेयस के परिप्रेक्ष्य से बेयस प्रमेय पर चर्चा करती है, डेविड जेसी मैकके द्वारा "सूचना सिद्धांत, आविष्कार और सीखना एल्गोरिदम" है। यह कैम्ब्रिज यूनिवर्सिटी प्रेस की किताब है, आईएसबीएन -13: 9780521642989। मेरा जवाब है (मुझे आशा है) पुस्तक में की गई चर्चाओं का एक प्रकार है। (सामान्य नियम लागू होते हैं: लेखक के साथ मेरा कोई जुड़ाव नहीं है, मुझे पुस्तक पसंद है)

Answer 7

अपने सबसे स्पष्ट रूप में बेयस प्रमेय केवल दो चीजों का पुन: कथन है:

1. $P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

तो समरूपता का उपयोग करके:

$$P(HD|I)=P(H|I)P(D|HI)=P(D|I)P(H|DI)$$

$P(D|I) \neq 0$$P(D|I)$ लेना:

$$P(H|DI)=P(H|I)\frac{P(D|HI)}{P(D|I)}$$

तो यही है? इतना सरल कुछ इतना भयानक कैसे हो सकता है? ज्यादातर चीजों के साथ "इसकी यात्रा जो गंतव्य से अधिक महत्वपूर्ण है"। बेयस प्रमेय चट्टानों कि तर्क के कारण यह करने के लिए नेतृत्व।

इससे जो चीज गायब है, वह है उत्पाद नियम और योग नियम $P(H|I)=1-P(\overline{H}|I)$, सुसंगत तर्क के स्वयंसिद्धों के आधार पर निगमनात्मक तर्क का उपयोग करके प्राप्त किया जा सकता है।

अब कटौतीत्मक तर्क में "नियम" यह है कि यदि आपके पास "ए का अर्थ बी" है, तो आपके पास "नॉट बी का मतलब ए नहीं है"। इसलिए हमारे पास "सुसंगत तर्क का अर्थ बेयस प्रमेय है"। इसका मतलब है "नॉट बायस प्रमेय का अर्थ है सुसंगत तर्क नहीं"। यानी यदि आपका परिणाम कुछ पूर्व और संभावना के लिए एक बायसीयन परिणाम के बराबर नहीं है तो आप असंगत रूप से तर्क कर रहे हैं।

इस परिणाम को कॉक्स प्रमेय कहा जाता है और 1940 में "संभावित संचय के बीजगणित" में सिद्ध किया गया था। प्रोएबिलिटी सिद्धांत में एक और हालिया व्युत्पत्ति दी गई है: विज्ञान का तर्क।

Answer 8

मुझे वास्तव में केविन मर्फी का परिचय Bayes Theorem http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

यहाँ उद्धरण एक अर्थशास्त्री लेख से है:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

बायेसियन दृष्टिकोण का सार यह बताने के लिए एक गणितीय नियम प्रदान करना है कि आपको नए सबूतों के प्रकाश में अपने मौजूदा विश्वासों को कैसे बदलना चाहिए। दूसरे शब्दों में, यह वैज्ञानिकों को अपने मौजूदा ज्ञान या विशेषज्ञता के साथ नए डेटा को संयोजित करने की अनुमति देता है। विहित उदाहरण यह कल्पना करना है कि एक नवजात शिशु अपने पहले सूर्यास्त का निरीक्षण करता है, और आश्चर्य करता है कि सूरज फिर से उठेगा या नहीं। वह दोनों संभावित परिणामों के लिए समान पूर्व संभाव्यता प्रदान करता है, और एक बैग में एक सफेद और एक काला संगमरमर रखकर इसका प्रतिनिधित्व करता है। अगले दिन, जब सूरज उगता है, तो बच्चा बैग में एक और सफेद संगमरमर रखता है। संभावना है कि बैग से बेतरतीब ढंग से गिरा हुआ एक संगमरमर सफेद होगा (यानी, भविष्य में बच्चों की सूर्योदय में विश्वास की डिग्री) इस प्रकार आधे से दो-तिहाई हो गई है। अगले दिन सूर्योदय के बाद, बच्चा एक और सफेद संगमरमर जोड़ता है, और संभावना (और इस प्रकार विश्वास की डिग्री) दो-तिहाई से तीन-चौथाई तक जाती है। और इसी तरह। धीरे-धीरे, प्रारंभिक विश्वास है कि सूरज बस के रूप में संभावना है कि हर सुबह उठने के लिए संशोधित नहीं है, एक निश्चितता बन जाती है कि सूरज हमेशा उगता रहेगा।