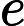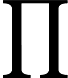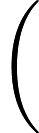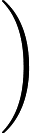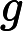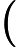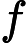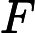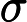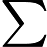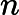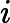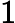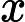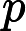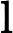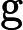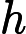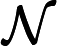अनुभवजन्य वितरण और गाऊसी मॉडल के बीच क्रॉस-एन्ट्रापी में क्यों चुकता त्रुटि है?

28

5.5 में, डीप लर्निंग (इयान गुडफेलो, योशुआ बेंगियो और आरोन कोर्टविल द्वारा), यह बताता है कि

एक नकारात्मक लॉग-लाइबिलिटी से युक्त कोई भी नुकसान प्रशिक्षण सेट और मॉडल द्वारा परिभाषित संभावना वितरण द्वारा परिभाषित अनुभवजन्य वितरण के बीच का अंतर-प्रवेश है। उदाहरण के लिए, मतलब चुकता त्रुटि अनुभवजन्य वितरण और गाऊसी मॉडल के बीच क्रॉस-एन्ट्रापी है।

मैं समझ नहीं पा रहा हूं कि वे समकक्ष क्यों हैं और लेखक बिंदु पर विस्तार नहीं करते हैं।

machine-learning normal-distribution cross-entropy

— मुफी ली
स्रोत

32

डेटा को । अनुभवजन्य वितरण के लिए लिखें । परिभाषा के अनुसार, किसी भी कार्य के लिए , $\mathbf{x}=(x_1, \ldots, x_n)$ $F(\mathbf{x})$ $f$

E_{F (x)} [f (X)] = \frac{1}{n} \sum_{i = 1}^{n} f (x_{i}) .

$\mathbb{E}_{F(\mathbf{x})}[f(X)] = \frac{1}{n}\sum_{i=1}^n f(x_i).$

बता दें कि मॉडल का घनत्व जहां को मॉडल के समर्थन पर परिभाषित किया गया है। क्रोस एंट्रोपी की और परिभाषित किया गया है होना करने के लिए $M$ $e^{f(x)}$ $f$ $F(\mathbf{x})$ $M$

\begin{matrix} (1) & H (F (x), M) = - E_{F (x)} [\log (e^{f (X)}] = - E_{F (x)} [f (X)] = - \frac{1}{n} \sum_{i = 1}^{n} f (x_{i}) . \end{matrix}

$H(F(\mathbf{x}), M) = -\mathbb{E}_{F(\mathbf{x})}[\log(e^{f(X)}] = -\mathbb{E}_{F(\mathbf{x})}[f(X)] =-\frac{1}{n}\sum_{i=1}^n f(x_i).\tag{1}$

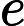
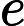
मान लें कि एक सरल यादृच्छिक नमूना है, तो इसका नकारात्मक लॉग संभावना है $x$

\begin{matrix} (2) & - \log (L (x)) = - \log \prod_{i = 1}^{n} e^{f (x_{i})} = - \sum_{i = 1}^{n} f (x_{i}) \end{matrix}

$-\log(L(\mathbf{x}))=-\log \prod_{i=1}^n e^{f(x_i)} = -\sum_{i=1}^n f(x_i)\tag{2}$

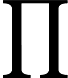
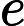
लघुगणक के गुणों के आधार पर (वे उत्पादों को रकम में बदलते हैं)। अभिव्यक्ति एक निरंतर बार अभिव्यक्ति । क्योंकि नुकसान कार्यों को केवल आंकड़ों में तुलना करके उपयोग किया जाता है, इससे कोई फर्क नहीं पड़ता है कि एक दूसरे के प्रति (सकारात्मक) लगातार है। यह इस अर्थ में है कि नकारात्मक लॉग संभावना "उद्धरण में एक क्रॉस-एंट्रोपी है। $(2)$ $n$ $(1)$

कोटेशन के दूसरे दावे को सही ठहराने के लिए थोड़ी और कल्पना की गई है। चुकता त्रुटि के साथ संबंध स्पष्ट है, क्योंकि "Gaussian मॉडल" के लिए, जो बिंदु पर को मान देता है, ऐसे किसी भी बिंदु पर का मान। $p(x)$ $x$ $f$

f (x; p, σ) = - \frac{1}{2} (\log (2 π σ^{2}) + \frac{(x - p (x))^{2}}{σ^{2}}),

$f(x; p, \sigma) = -\frac{1}{2}\left(\log(2\pi \sigma^2) + \frac{(x-p(x))^2}{\sigma^2}\right),$

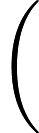
जो चुकता त्रुटि लेकिन द्वारा rescaled और एक फ़ंक्शन द्वारा स्थानांतरित कर दिया गया है । उद्धरण को सही बनाने का एक तरीका यह है कि यह "मॉडल" के भाग पर विचार नहीं करता है - को किसी भी तरह डेटा से स्वतंत्र रूप से निर्धारित किया जाना चाहिए। उस मामले में मतभेद मतलब वर्ग त्रुटियों के बीच के लिए आनुपातिक हैं मतभेद पार entropies या लॉग-likelihoods के बीच है, जिससे मॉडल फिटिंग प्रयोजनों के लिए सभी तीन बराबर बना रही है। $(x-p(x))^2$ $1/(2\sigma^2)$ $\sigma$ $\sigma$ $\sigma$

(आमतौर पर, हालांकि, मॉडलिंग प्रक्रिया के भाग के रूप में फिट है, इस मामले में उद्धरण काफी सही नहीं होगा।) $\sigma = \sigma(x)$

— व्हीबर
स्रोत

1

+1 दो सुझाव के साथ - साथ भ्रम से बचने के लिए बजाय उपयोग कर सकता है । दूसरा का सबसे अनुमान है कि । जब आप इसे प्लग इन करते हैं और इसे जोड़ते हैं तो आपको मिलता है । AIC प्रकार सूत्र की तरह ही ...

g ()

$g ()$

f ()

$f ()$

F ()

$F ()$

σ^{2}

$\sigma^2$

k \sum_{i = 1}^{n} {(x_{i} - p (x_{i}))}^{2}

$k\sum_{i=1}^n \left (x_i - p (x_i)\right)^2$

- \frac{1}{2} \log [\sum_{i = 1}^{n} {(x_{i} - p (x_{i}))}^{2}] + h (k)

$-\frac {1}{2}\log\left [\sum_{i=1}^n \left (x_i - p (x_i)\right)^2\right] +h(k)$

— probabilityislogic

@probabilityislogic मैं जोड़ी चुनें और क्योंकि वे करते बारीकी से संबंधित मात्रा प्रतिनिधित्व करते हैं।

F

$F$

f

$f$

— whuber

नमस्ते, मुझे लगता है कि यह केवल रैखिक वितरण पर लागू होता है। Nonlinear वितरण समस्याओं में, मुझे लगता है कि हम अभी भी लागत समारोह के रूप में MSE का उपयोग कर सकते हैं, है ना?

— सिंह लाई

5

दीप लर्निंग पुस्तक के पाठकों के लिए, मैं उत्कृष्ट स्वीकार किए गए उत्तर को जोड़ना चाहूंगा कि लेखकों ने अपने वक्तव्य को खंड 5.5.1 में विस्तार से समझाया है। उदाहरण के लिए: रैखिक प्रतिगमन अधिकतम संभावना के रूप में ।

वहां, वे स्वीकार किए गए उत्तर में वर्णित बाधा की सूची देते हैं:

$p(y | x) = \mathcal{N}\big(y; \hat{y}(x; w), \sigma^2\big)$ । फ़ंक्शन गौसियन के माध्य की भविष्यवाणी देता है। इस उदाहरण में, हम मानते हैं कि उपयोगकर्ता द्वारा चुने गए कुछ स्थिर लिए विचरण तय है । $\hat{y}(x; w)$ $\sigma^2$

फिर, वे दिखाते हैं कि MSE का न्यूनतमकरण अधिकतम संभावना अनुमान से मेल खाता है और इस प्रकार अनुभवजन्य वितरण और बीच क्रॉस-एन्ट्रापी का न्यूनतमकरण होता है । $p(y|x)$

— किलियन बैट्ज़नर
स्रोत