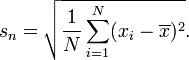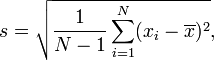यूएस और यूके स्कूल मानक विचलन की गणना के विभिन्न तरीकों को क्यों सिखाते हैं?

15

जैसा कि मैं समझता हूं कि यूके के स्कूल सिखाते हैं कि मानक विचलन का उपयोग करते हुए पाया जाता है:

$वैकल्पिक शब्द$

जबकि यूएस स्कूल सिखाते हैं:

$वैकल्पिक शब्द$

(वैसे भी एक बुनियादी स्तर पर)।

इससे अतीत में मेरे छात्रों की कई समस्याएं पैदा हुई हैं क्योंकि उन्होंने इंटरनेट पर खोज की है, लेकिन गलत स्पष्टीकरण पाया है।

अंतर क्यों?

सरल डेटासेट के साथ 10 मान कहते हैं, यदि गलत पद्धति लागू होती है (जैसे कि एक परीक्षा में) तो त्रुटि की क्या डिग्री होगी?

— अमोस
स्रोत

4

मुझे यकीन नहीं है कि 'गलत' फॉर्मूला के रूप में एक या दूसरे का चरित्र चित्रण मुद्दे को समझने का तरीका है। यह सिर्फ इतना है कि दूसरा इस मायने में 'बेहतर' है कि यह सही मानक विचलन का निष्पक्ष अनुमान लगाने वाला है। इसलिए, यदि आप निष्पक्ष अनुमानों की परवाह करते हैं, तो दूसरा 'बेहतर' / 'सही' है।

मैं सूत्र को "गलत" के रूप में विशुद्ध रूप से इस रूप में चिह्नित कर रहा था कि एक परीक्षा में यदि आप उस सूत्र का उपयोग करते हैं जो पाठ्यक्रम द्वारा फेल नहीं किया जाता है तो आप "गलत" उत्तर के साथ समाप्त हो जाएंगे। साथ ही अगर मान प्रति जनसंख्या जनसंख्या का नमूना नहीं हैं तो निश्चित रूप से पहला सूत्र अधिक सटीक मूल्य देता है।

— आमोस

14

श्रीकांत, मुझे नहीं लगता कि दूसरा कोई निष्पक्ष अनुमानक है। इसका वर्ग सत्य विचरण का एक निष्पक्ष अनुमानक है। हालांकि, जेन्सेन की असमानता यह स्थापित करती है कि एक यादृच्छिक चर के वक्रता फ़ंक्शन की अपेक्षा यादृच्छिक चर की अपेक्षा के कार्य के समान नहीं है। इसलिए दूसरा सूत्र सच्चे मानक विचलन का निष्पक्ष अनुमानक नहीं हो सकता है।

— एंड्रयू रॉबिन्सन

क्रॉस-रेफरेंस के लिए: यह भी पूछा गया @ m.SE ...

— JM एक स्टेटिस्टिशियन नहीं है

4

द्वारा फ्रीडमैन, Pisani, और पूर्वेस बहुत लोकप्रिय प्राथमिक पाठ का उपयोग कर किसी भी अमेरिका स्कूल पहले सूत्र (उपयोग कर रहा है

,) तो यह एक अमेरिका बनाम ब्रिटेन अंतर के रूप में यह चिह्नित करने के लिए गलत लगता है।

s_{n}

$s_n$

— whuber

18

पहला सूत्र जनसंख्या मानक विचलन है और दूसरा सूत्र नमूना मानक विचलन है। दूसरा सूत्र भी विचरण के निष्पक्ष अनुमानक से संबंधित है - आगे के विवरण के लिए विकिपीडिया देखें।

मुझे लगता है कि यहाँ (यूके में) वे हाई स्कूल में नमूना और आबादी के बीच अंतर नहीं करते हैं। वे निश्चित रूप से पक्षपाती अनुमानकों जैसी अवधारणाओं को नहीं छूते हैं।

— csgillespie
स्रोत

4

कॉलिन, मानक विचलन के एक निष्पक्ष अनुमानक के पास सामान्य मामले में एक बंद प्रपत्र प्रतिनिधित्व नहीं है। जो मौजूद है वह इस मामले में विचरण (s 2 ) का निष्पक्ष अनुमानक है। उल्लेखनीय है कि दोनों जनसंख्या विचलन के निरंतर अनुमानक हैं - और इसलिए निरंतर मानचित्रण प्रमेय द्वारा, मानक विचलन के दो अनुमानक हैं। एक संबंधित बिंदु यह है कि s n 2 का MS <s> 2 से कम MSE है। निष्पक्षता थोपने से अतिरिक्त फायदा यकीनन मिलता है।

— मॉर्निंगटन

@ तीर्थंकर - बहुत मैला। मैंने उत्तर को थोड़ा बदल दिया है। धन्यवाद।

— csgillespie

2

जहाँ तक मुझे याद है, मुझे GCSE गणित और विज्ञान (14-16 आयु) में 'नमूना' गणना सिखाई गई थी और आबादी और नमूनों के बीच अंतर और उनके संबद्ध विचरण उपायों को कवर किया गया था (हालांकि गहराई में नहीं) उम्र 16-18)। इसलिए मुझे यकीन नहीं है कि यह एक साधारण यूके / यूएस अंतर है।

— फ्रेया हैरिसन

11

क्योंकि किसी ने भी अभी तक अंतिम प्रश्न का उत्तर नहीं दिया है - अर्थात्, दो सूत्रों के बीच अंतर को निर्धारित करने के लिए - चलो इसका ध्यान रखें।

कई कारणों से, उनके अंतर के बजाय उनके अनुपात के संदर्भ में मानक विचलन की तुलना करना उचित है । अनुपात है

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

$|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ एसडी, जैसे दो डेटासेट के प्रसार की तुलना करते समय। (जब डेटासेट समतुल्य होते हैं, तो विसंगतियां प्रभावी रूप से पूरी तरह से गायब हो जाती हैं और दोनों फार्मूले निष्कर्ष तक ले जाते हैं।) तर्क है, ये तर्क के रूप हैं जो हम शुरुआती छात्रों को पढ़ाने की कोशिश कर रहे हैं, इसलिए यदि छात्र इस बारे में चिंतित हैं कि किस सूत्र का उपयोग करना है। यह एक संकेत के रूप में लिया जा सकता है कि पाठ या वर्ग इस बात पर जोर देने में विफल हो रहा है कि वास्तव में क्या महत्वपूर्ण है।

$N$ $t$ $z$ $s$ $s_n$

— व्हीबर
स्रोत

6

यह बेसेल का सुधार है । अमेरिकी संस्करण नमूना मानक विचलन के लिए सूत्र दिखा रहा है , जहां ऊपर यूके संस्करण नमूना का मानक विचलन है ।

— रीड कोपसी
स्रोत

5

मुझे यकीन नहीं है कि यह विशुद्ध रूप से एक अमेरिकी बनाम ब्रिटिश मुद्दा है। इस पृष्ठ के शेष भाग को मैंने लिखे एक faq से उद्धृत किया है। ( http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 )।

भाजक में n-1 के साथ एसडी की गणना कैसे करें

प्रत्येक मूल्य और नमूना माध्य के बीच अंतर के वर्ग की गणना करें।
उन मूल्यों को जोड़ें।
योग को n-1 से विभाजित करें। परिणाम को विचरण कहा जाता है।
मानक विचलन प्राप्त करने के लिए वर्गमूल लें।

क्यों एन -1?

मानक विचलन की गणना करते समय n के बजाय n-1 से विभाजित क्यों करें? चरण 1 में, आप प्रत्येक मान और उन मानों के बीच अंतर की गणना करते हैं। आप जनसंख्या का सही अर्थ नहीं जानते हैं; आप सभी जानते हैं कि आपके नमूने का मतलब क्या है। ऐसे दुर्लभ मामलों को छोड़कर जहां नमूना माध्य जनसंख्या माध्य के बराबर होता है, डेटा सैंपल माध्य के अधिक समीप होगा, क्योंकि यह वास्तविक जनसंख्या माध्य होगा। तो चरण 2 में आपके द्वारा गणना की जाने वाली मान शायद थोड़ी छोटी होगी (और इससे बड़ी नहीं हो सकती) यदि आप सही जनसंख्या का उपयोग चरण 1 में करते हैं तो इससे क्या होगा। इसके लिए बनाने के लिए, n-1 से विभाजित करें nv की तुलना में इसे बेसेल के सुधार कहा जाता है।

लेकिन एन -1 क्यों? यदि आप नमूना का मतलब जानते हैं, और सभी लेकिन मूल्यों में से एक है, तो आप गणना कर सकते हैं कि अंतिम मूल्य क्या होना चाहिए। सांख्यिकीविदों का कहना है कि स्वतंत्रता के लिए एन -1 डिग्री हैं।

SD को n-1 के बजाय n के एक हर के साथ गणना की जानी चाहिए।

सांख्यिकी किताबें अक्सर एसडी की गणना करने के लिए दो समीकरण दिखाती हैं, एक एन का उपयोग करते हुए, और दूसरा एन -1 का उपयोग करते हुए, भाजक में। कुछ कैलकुलेटर में दो बटन होते हैं।

N-1 समीकरण का उपयोग सामान्य स्थिति में किया जाता है जहां आप डेटा के नमूने का विश्लेषण कर रहे हैं और अधिक सामान्य निष्कर्ष बनाने की इच्छा रखते हैं। एसडी इस तरह से गणना (भाजक में एन -1 के साथ) समग्र आबादी में एसडी के मूल्य के लिए आपका सबसे अच्छा अनुमान है।

यदि आप केवल डेटा के किसी विशेष सेट में भिन्नता को निर्धारित करना चाहते हैं, और व्यापक निष्कर्ष बनाने के लिए अतिरिक्त रूप से योजना नहीं बनाते हैं, तो आप हर में n का उपयोग करके एसडी की गणना कर सकते हैं। परिणामी SD उन विशिष्ट मानों का SD है। एसडी को इस तरह से गणना करने का कोई मतलब नहीं है यदि आप उस आबादी के एसडी का अनुमान लगाना चाहते हैं जिससे उन बिंदुओं को खींचा गया था। यह केवल भाजक में n का उपयोग करने के लिए समझ में आता है जब आबादी से कोई नमूना नहीं होता है, सामान्य निष्कर्ष बनाने की कोई इच्छा नहीं होती है।

विज्ञान का लक्ष्य लगभग हमेशा सामान्य करना है, इसलिए हर में n के साथ समीकरण का उपयोग नहीं किया जाना चाहिए। एकमात्र उदाहरण मैं सोच सकता हूं कि यह कहां समझ में आता है कि परीक्षा के अंकों के बीच भिन्नता को निर्धारित किया जा सकता है। लेकिन बहुत बेहतर होगा कि हर स्कोर, या फ़्रीक्वेंसी डिस्ट्रीब्यूशन हिस्टोग्राम का स्कैप्लेट दिखाया जाए।

— हार्वे मोटुलस्की
स्रोत

1

मैं यह सुझाव नहीं दे रहा था, मैं बस इस बात से उत्सुक था कि ऐसा अंतर क्यों उत्पन्न हो सकता है, गलत सलाह के बाद किस प्रकार की त्रुटि हो सकती है और क्या अंतर का एक अच्छा स्पष्टीकरण था जो मैं अपने छात्रों को दे सकता था। ।

— आमोस

@harvey - लिंक मृत है

— baxx

1

@baxx .. इसे इंगित करने के लिए धन्यवाद। फिक्स्ड।

— हार्वे मोटुलस्की

3

चूँकि N डेटा सेट में अंकों की संख्या है, इसलिए कोई यह तर्क दे सकता है कि किसी ने माध्य की गणना करके डेटा में स्वतंत्रता की डिग्री को एक से कम कर दिया है (क्योंकि किसी ने डेटा सेट में एक निर्भरता शुरू की है), इसलिए किसी को एन का उपयोग करना चाहिए -1 जब एक डेटा सेट से मानक विचलन का अनुमान लगाते हैं जिसके लिए किसी को पहले मतलब का अनुमान लगाना था।

— बेंजामिन बैनियर
स्रोत