PCA प्लॉट के पच्चर जैसा आकार क्या दर्शाता है?

Question

पाठ के वर्गीकरण के लिए ऑटोएन्कोडर्स पर अपने पेपर में हिंटन और सलाखुद्दीनोव ने 2-आयामी एलएसए (जो पीसीए से निकटता से संबंधित है) द्वारा निर्मित भूखंड का प्रदर्शन किया :।

पीसीए को बिल्कुल अलग उच्च आयामी डेटा पर लागू करना मैंने एक समान दिखने वाला प्लॉट प्राप्त किया: (इस मामले को छोड़कर मैं वास्तव में जानना चाहता था कि क्या कोई आंतरिक संरचना है)।

यदि हम पीसीए में यादृच्छिक डेटा फ़ीड करते हैं तो हम एक डिस्क के आकार का बूँद प्राप्त करते हैं, इसलिए यह पच्चर के आकार का आकार यादृच्छिक नहीं है। क्या इसका अपने आप से कोई मतलब है?

Comments

मुझे लगता है कि सभी चर सकारात्मक (या गैर-नकारात्मक) और निरंतर हैं? यदि ऐसा है, तो कील के किनारे सिर्फ ऐसे बिंदु हैं जिनके आगे डेटा 0 / ऋणात्मक हो जाएगा। इसके अलावा, आप उसी पैटर्न को प्राप्त कर सकते हैं जिसे आप सकारात्मक दाएं तिरछा चर दिखाते हैं; अवलोकन कम अंत में टकरा रहे हैं। यदि आपके पास सकारात्मक समरूप यादृच्छिक चर हैं तो आपको एक (घुमाया हुआ) वर्ग दिखाई देगा। इसलिए आपके द्वारा दिखाए गए पैटर्न जैसे डेटा पर सिर्फ अड़चनें हैं। अन्य पैटर्न एक घोड़े की नाल की तरह दिखाई दे सकते हैं, लेकिन ये चर की सीमाओं पर बाधाओं के कारण नहीं हैं।

— गैविन सिम्पसन

@GavinSimpson यह एक टिप्पणी से काफी अधिक है। इसका उत्तर में विस्तार क्यों नहीं?

— माइक हंटर

मैंने अपने बच्चों से (3 और 4 साल) पूछा कि ये तस्वीरें उन्हें क्या याद दिलाती हैं और उन्होंने कहा कि यह एक मछली है। तो शायद "मछली जैसी आकृति"?

— अमीबा

@GavinSimpson, धन्यवाद! दोनों मामलों में चर वास्तव में गैर-नकारात्मक होते हैं, बॉट भी दोनों मामलों में वे पूर्णांक मूल्यवान हैं। क्या यह कुछ बदलता है?

— मैकलेगिन

Answer 1

यह मानते हुए कि चर सकारात्मक या गैर-नकारात्मक हैं, किनारे के किनारे केवल ऐसे बिंदु हैं जिनके आगे डेटा क्रमशः 0 या नकारात्मक हो जाएगा। जैसे-जैसे वास्तविक जीवन के आंकड़े सही तिरछे होते जाते हैं, हमें उनके वितरण के निचले छोर पर बिंदुओं का अधिक घनत्व दिखाई देता है और इसलिए कील के "बिंदु" पर अधिक घनत्व होता है।

अधिक आम तौर पर, पीसीए केवल डेटा का एक रोटेशन होता है और उन डेटा पर बाधाएं आम तौर पर प्रिंसिपल घटकों में उसी तरह दिखाई देती हैं जैसे कि प्रश्न में दिखाया गया है।

यहां कई लॉग-सामान्य रूप से वितरित चर का उपयोग करके एक उदाहरण दिया गया है:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

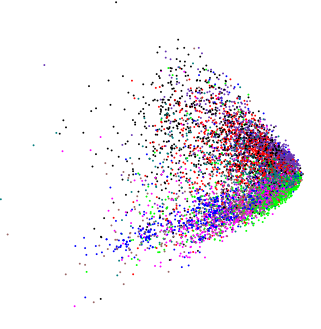
पहले दो पीसी द्वारा निहित रोटेशन के आधार पर, आप पच्चर को देख सकते हैं या आप कुछ अलग संस्करण देख सकते हैं, यहां 3 डी का उपयोग करके दिखा सकते हैं ( ordirgl()के स्थान पर plot())

यहां, 3 डी में हम केंद्र के द्रव्यमान से फैलते हुए कई स्पाइक्स देखते हैं।

गाऊसी यादृच्छिक चर के लिए ($X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$) जहां प्रत्येक का एक ही माध्य और विचरण होता है, हमें बिंदुओं का एक क्षेत्र दिखाई देता है

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

और समान सकारात्मक यादृच्छिक चर के लिए हम एक घन देखते हैं

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

ध्यान दें कि यहाँ चित्रण के लिए, मैं केवल 3 यादृच्छिक चर का उपयोग करके वर्दी दिखाता हूं इसलिए अंक 3 डी में एक घन का वर्णन करते हैं। उच्च आयाम / अधिक चर के साथ हम 5 डी हाइपरक्यूब को पूरी तरह से 3 डी में नहीं दिखा सकते हैं और इसलिए अलग "क्यूब" आकार कुछ हद तक विकृत हो जाता है। इसी तरह के मुद्दे दिखाए गए अन्य उदाहरणों को प्रभावित करते हैं, लेकिन उन उदाहरणों में बाधाओं को देखना अभी भी आसान है।

आपके डेटा के लिए, PCA से पहले वेरिएबल्स का एक लॉग ट्रांसफ़ॉर्म पूंछों में खींच जाएगा और क्लैंप किए गए डेटा को बाहर खींच देगा, जैसे कि आप एक रैखिक रिग्रेशन में इस तरह के ट्रांसफ़ॉर्मेशन का उपयोग कर सकते हैं।

अन्य आकार पीसीए भूखंडों में फसल कर सकते हैं; ऐसा ही एक आकार पीसीए में संरक्षित मीट्रिक प्रतिनिधित्व का एक गुण है और इसे घोड़े की नाल के रूप में जाना जाता है । एक लंबी या प्रमुख ढाल के साथ डेटा के लिए (नमूने 0 से अधिकतम तक बढ़ते हुए चर के साथ एक एकल आयाम के साथ व्यवस्थित किए गए और फिर से 0 तक घटने के साथ डेटा के कुछ हिस्सों को इस तरह के कलाकृतियों को उत्पन्न करने के लिए अच्छी तरह से जाना जाता है।

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

जो एक अत्यधिक घोड़े की नाल का उत्पादन करता है, जहां कुल्हाड़ियों के सिरों पर बिंदु बीच में झुकते हैं।

Comments

+1। यह आपके स्वयं के उत्तर से लिंक करने के लिए समझ में आ सकता है कि पीसीए / पत्राचार विश्लेषण में "घोड़े की नाल प्रभाव" और / या "आर्च प्रभाव" क्या है? इस उत्तर के अंतिम भाग में।

— अमीबा