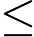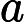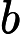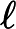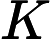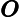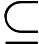में समस्याएं

Question

क्या समस्याओं से संबंध रखते हैं के लिए जाना जाता लेकिन से संबंधित ज्ञात नहीं पी ?$\mathsf{BPP}$$\mathsf P$

अधिक सटीक रूप से, मैं स्वतंत्र समस्याओं में दिलचस्पी रखता हूं , वह है जिसका व्युत्पन्नकरण समतुल्य नहीं माना जाता है। उदाहरण के लिए, यह ज्ञात है कि पीआईटी और बहुभिन्नरूपी बहुपद गुणनखंड व्युत्पन्न समान हैं और मैं उन्हें केवल एक समस्या के रूप में गिना जाऊंगा ।

मेरे सवाल का प्रेरणा है कि यह है कि कहने के लिए आम बात है है "वहाँ में कुछ समस्याएं हैं नहीं में माने जाते पी "$\mathsf{BPP}$$\mathsf{P}$ , लेकिन मैं उन्हें की एक सूची को खोजने के लिए सक्षम नहीं था। विशेष रूप से, अगर मुझे इस श्रेणी में समस्याओं का हवाला देना है, तो मैं आम तौर पर परिमित क्षेत्रों पर बहुभिन्नरूपी बहुपद के गुणनखंड या बहुभिन्नरूपी बहुपद के कारक का हवाला देता हूं। मुझे लगता है कि ऐसे उदाहरण मौजूद हैं जो बहुपद के कारक से संबंधित नहीं हैं, उदाहरण के लिए अन्य डोमेन जैसे कि ग्राफ सिद्धांत या औपचारिक भाषा सिद्धांत।

पुनश्च: मैं उत्सुक हूं कि इस वेबसाइट पर एक समान प्रश्न मौजूद नहीं है। मेरी क्षमा याचना अगर मुझे यह नहीं मिला (या उन्हें)!

Comments

इस पोस्ट के उत्तर में दो उदाहरण हैं cstheory.stackexchange.com/questions/11425/…

— मोहम्मद अल-तुर्किस्टनी

Answer 1

यदि आप स्वतंत्र समस्याओं के बारे में पूछ रहे हैं, तो कैसे:

अंतराल में एक प्रमुख का पता लगाएं , दो अपराधों का पता लगाएं , जिनके उत्पाद अंतराल में हैं [ एन , 9 एन / 8 ] , उन तीन अपराधों का पता लगाएं जिनके उत्पाद अंतराल में हैं [ एन , 17 एन / 16 ] , चार प्राइम खोजें जिनके उत्पाद अंतराल में हैं [ एन , 33 एन / 32 ] , पांच प्राइम खोजें जिनके उत्पाद अंतराल में हैं [ एन $[N, 5N/4]$
$[N, 9N/8]$
$[N, 17N/16]$
$[N, 33N/32]$
, … ।$[N, 65N/64]$
$\ldots$

यह बहुत अधिक संभावना है कि यदि आपके पास वास्तव में इनमें से पहले को हल करने के लिए एक बहुपद एल्गोरिथ्म था, तो आपके पास उन सभी के लिए एक बहुपद एल्गोरिथ्म होगा। लेकिन मैं यह नहीं देखता कि औपचारिक रूप से इनमें से किसी को भी कैसे कम किया जाए। बेशक, समस्या

अंतराल में एक प्रधानमंत्री का पता लगाएं $[N, N+\log^{17} N ]$

इन सभी को हल करता है।

Comments

सटीक होने के लिए, आपके मन में इन समस्याओं का निर्णय संस्करण क्या है? धन्यवाद।

— usul

@सुल: मेरे पास इन समस्याओं का निर्णय संस्करण नहीं है। क्या मुझे यह करना ज़रूरी है? मुझे एहसास है कि तकनीकी रूप से, BPP में केवल निर्णय की समस्याएं होती हैं। ज्यादातर समय, निर्णय की समस्याएं और फ़ंक्शन समस्याएं कम या ज्यादा समतुल्य होती हैं, जिसका अर्थ है कि आप सामान्यता के नुकसान के बिना सिर्फ निर्णय की समस्याओं पर विचार कर सकते हैं। मुझे यकीन नहीं है कि यह इस सवाल के लिए सच है, और मुझे नहीं पता कि ओपी केवल निर्णय की समस्याओं के बारे में परवाह करता है या नहीं।

— पीटर शोर

मैं सिर्फ इसलिए पूछ रहा हूं क्योंकि महत्वपूर्ण सूक्ष्मताएं आने पर मुझे ठीक से पता नहीं है। मुझे लगता है कि कुछ फ़ंक्शन समस्याएं होनी चाहिए जो बिना शर्त के "बीपीपी" में जानी जाती हैं और "पी" नहीं हैं, उदाहरण के लिए कोलमोगोरोव जटिलता (?) की एक स्ट्रिंग का उत्पादन करें । इसलिए मुझे लगा कि प्रश्न निर्णय की समस्याओं की ओर इशारा करेगा, और सोच रहा था कि क्या आपके उत्तर (वर्तमान ज्ञान) का एक वैध निर्णय संस्करण होगा "जैसे कि [ N , 5 N / 4 ] में एक प्रमुख है ?" $n$$[N,5N/4]$

— usul

@सुल: इस सवाल के लिए: "क्या में एक प्रमुख है ?", यह ज्ञात है कि एक निरंतर-समय एल्गोरिथ्म मौजूद है। ऐसा लग रहा है: कहते हैं "हाँ" जब एन > 10 6 और स्पष्ट रूप से जाँच जब एन ≤ 10 6 । इसे सिद्ध करने के लिए आपको कुछ संख्या सिद्धांत की आवश्यकता है । $[N, 5N/4]$$N > 10^6$$N \leq 10^6$

— पीटर शोर

ठीक है, निश्चित / ठीक है। मुझे लगता है कि मैं इस सवाल में केव की टिप्पणी से सहमत हूं कि एक प्राकृतिक संगत निर्णय समस्या है, दिया गया है , क्या [ ए , बी ] में एक प्रमुख है ? $a,b$$[a,b]$

— usul

Answer 2

यादृच्छिकता का एक विशेष उपयोग है जो कि मानकीकृत जटिलता में काफी आम है, जिसमें या तो अलगाव लेम्मा , या श्वार्ट्ज-ज़िप्पल लेम्मा शामिल है । मोटे तौर पर, इसमें संभावित समाधानों की एक बड़ी गणना को परिभाषित करना शामिल है, और यह तर्क देते हुए कि सभी गैर-समाधान "जोड़ी अप" (जैसे, दो बार गिने जाते हैं) जबकि वांछित समाधान (ओं) को केवल एक बार गिना जाता है। फिर एक या तो केवल एक सबसे छोटे समाधान के साथ एक स्थिति उत्पन्न करने के लिए अलगाव लेम्मा का उपयोग करता है, या GF ऊपर एक बड़ी संगत औपचारिक बहुपद को परिभाषित करता है और किसी भी गैर-युग्मित शब्द का परीक्षण करने के लिए Schwartz-Zippel का उपयोग करता है। (मुझे यकीन है कि वहाँ एक अच्छा अवलोकन या सर्वेक्षण है, लेकिन फिलहाल यह मेरे दिमाग को खिसकाता है।)$(2^\ell)$

उन्होंने कहा, मैं केवल दो मामलों के बारे में सोच सकता हूं जहां इस उपयोग से बीपीपी और पी के बीच अंतर होगा।

सबसे पहले लघु एल्गोरिथ्म के लिए हाल ही में एल्गोरिथ्म है दो लेखक पथ ( लेखक का पीडीएफ ), Björklund और Husfeldt, ICALP 2014।

दूसरी एक मानकीकृत समस्या है - एक ग्राफ में निर्दिष्ट तत्वों के सेट K के माध्यम से एक सरल चक्र ढूंढें, अर्थात, एक स्टेनर चक्र समस्या जैसी कोई चीज। कब , यह समस्या Björklund, Husfeldt, Taslaman, Soda 2012 ( लिंक ) द्वारा BPP में है । (एक पिछले नियतात्मक एल्गोरिथ्म है, लेकिन इसकी निर्भरता | K | घातीय रूप से बदतर है।) इस प्रकार, कोई भी समस्या "लॉग-स्टाइनर साइकिल" (या जिसे आप इसे कॉल करना चाहते हैं) को परिभाषित कर सकता है, और यह एक प्रश्न फिट होगा।$|K|=O(\log n)$$|K|$

Answer 3

मैं एक विशेषज्ञ नहीं हूं, लेकिन शायद कुछ (नहीं-तो-प्राकृतिक)? उदाहरण सीधे बीपीपी निर्णय समस्याओं के बीपीपी खोज समस्याओं को कम करने की तकनीक का उपयोग करके सीधे प्राप्त किए जा सकते हैं , जो प्रस्तुत हैं:

Oded Goldreich, P = BPP की दुनिया में। जटिलता और क्रिप्टोग्राफी 2011 में अध्ययन: 191-232

विशेष रूप से प्रमेय 3.5 देखें : (निर्णय के लिए खोज को कम करना): प्रत्येक BPP- खोज समस्या , एक द्विआधारी संबंध R मौजूद है जैसे R y e s ⊆ R ⊆ ( { 0 , 1) } * × { 0 , 1 } * ) ∖ आर एन ओ और की तलाश की समस्या को हल $(R_{yes},R_{no})$$R$$R_{yes} \subseteq R \subseteq (\{0, 1\}^∗ \times \{0, 1\}^∗) \setminus R_{no}$$R$BPP में कुछ निर्णायक समस्या के लिए नियतात्मक रूप से reducible है, जिसे निरूपित किया गया है । इसके अलावा, कमी के समय जटिलता के लिए समाधान खोजने का संभाव्य समय-जटिलता में रेखीय है ( आर वाई ई एस , आर एन ओ ) , जबकि की संभाव्य समय-जटिलता Π एक द्विघातीय बहुपद और संभाव्य का उत्पाद है निर्णय प्रक्रिया की समय-जटिलता ( R y e s , R n o ) के लिए ।$\Pi$$(R_{yes},R_{no})$$\Pi$$(R_{yes},R_{no})$

प्रमेय को सामान्य निर्माण समस्याओं के लिए बढ़ाया जा सकता है, उदाहरण के लिए ( कोरोलरी 3.9 देखें ) एक बड़े पर्याप्त अंतराल में एक प्रमुख खोजने की समस्या पर विचार करें:

किसी निश्चित के लिए , पर इनपुट एन , अंतराल में एक प्रमुख लगता है [ एन , एन + एन सी$c > 7/12$$N$$[N, N + N^c]$

यादृच्छिक एल्गोरिदम अपेक्षित बहुपद समय में चलता है; कोई नियतात्मक बहुपद समय एल्गोरिथ्म ज्ञात नहीं है; लेकिन अगर BPP = P ऐसे नियतात्मक बहुपद समय एल्गोरिथ्म मौजूद होना चाहिए (क्योंकि यह BPP- निर्णय की समस्या को कम किया जा सकता है)।