शायद एल्गोरिथ्म ही वह अस्पष्ट नहीं है, लेकिन जो वास्तव में व्यवहार में उपयोग किए जाने वाले कार्यान्वयन को नाम दे सकता है? हाँ मैं!
TIGCC (TI-89/92 / V200 रेखांकन कैलकुलेटर के लिए एक GCC- आधारित संकलक) qsortअपने मानक पुस्तकालय में कार्यान्वयन के लिए शैल प्रकार का उपयोग करता है :
__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
unsigned short gap,byte_gap,i,j;
char *p,*a,*b,temp;
for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1) // Yes, this is not a quicksort,
{ // but works fast enough...
byte_gap=gap*(unsigned short)size;
for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
{
a=p; b=p+byte_gap;
if(cmp_func(a,b)<=0) break;
for(j=size;j;j--)
temp=*a, *a++=*b, *b++=temp;
}
}
}
शैल आकार कोड आकार को कम रखने के लिए क्विकॉर्ट के पक्ष में चुना गया था। यद्यपि यह विषमतापूर्ण जटिलता है, लेकिन TI-89 में RAM (190K, कार्यक्रम का आकार और किसी भी अनारक्षित चर के कुल आकार) की पूरी मात्रा नहीं है, इसलिए यह मान लेना सुरक्षित है कि मदों की संख्या नीचे।
मेरे द्वारा लिखित एक कार्यक्रम में बहुत धीमी गति से होने की शिकायत के बाद एक तेज कार्यान्वयन लिखा गया था। यह असेंबली ऑप्टिमाइजेशन के साथ बेहतर गैप साइज का उपयोग करता है। यह यहाँ पाया जा सकता है: qsort.c
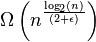 के लिए ε > 0।
के लिए ε > 0।