बलोच क्षेत्र में जेड गेट के बारे में कैसे सोचें?

Question

मैं उलझन में हूं कि कैसे समझें $Z$ एक बलोच क्षेत्र में गेट।

मैट्रिक्स को ध्यान में रखते हुए $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ यह समझ में आता है $Z|0\rangle = |0\rangle$ तथा $Z|1\rangle = -|1\rangle$।

यह यहाँ बताया गया है$Z$ गेट है $\pi$ चारों ओर घूमना $Z$एक्सिस। फिर, मैं कैसे समझूं$Z|1\rangle = -|1\rangle$? जबसे$|1\rangle$ दक्षिणी ध्रुव है, मुझे लगता है कि ऐसा सोचना स्वाभाविक है $\pi$ चारों ओर घूमना $Z$ अक्ष कुछ भी नहीं करता है।

Answer 1

बलोच क्षेत्र के बारे में सोचने का तरीका राज्य के लिए घनत्व मैट्रिक्स के संदर्भ में है। $Z$ या तो अभिनय $|0\rangle\langle 0|$ या $|1\rangle\langle 1|$कुछ भी नहीं करता है, जैसा कि किसी भी विकर्ण घनत्व मैट्रिक्स के लिए सच है। रोटेशन के प्रभाव को देखने के लिए, आपको यह देखने की जरूरत है कि किसी भी गैर-विकर्ण घनत्व मैट्रिक्स द्वारा कैसे बदला जाता है$Z$, जैसे कि $|+\rangle\langle +|$।

Answer 2

$|1\rangle$ तथा $-|1\rangle$बलोच क्षेत्र पर एक ही बिंदु को सौंपा गया है क्योंकि वे वैश्विक चरण के बराबर हैं । बीजगणित:$|1\rangle \equiv -|1\rangle$ कहाँ पे $\equiv$"वैश्विक चरण के बराबर" का अर्थ है। मतलब कुछ है$\theta$ ऐसा है कि $-|1\rangle = e^{i \theta} |1\rangle$।

जो चीज आपको भ्रमित कर रही है, वह इस तथ्य के बावजूद है $|0\rangle \equiv Z |0\rangle$ तथा $|1\rangle \equiv Z |1\rangle$, यह दोनों के रैखिक संयोजनों के लिए सही नहीं है। उदाहरण के लिए,$Z |+\rangle \not\equiv Z |+\rangle$ भले ही $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$।

Answer 3

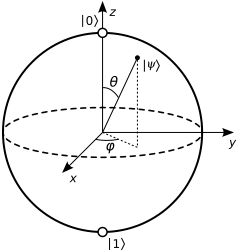
विकिपीडिया के अनुसार , हम किसी भी शुद्ध स्थिति को लिख सकते हैं

$$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$$

कहाँ पे $\theta$ तथा $\phi$ बलोच क्षेत्र पर कोण हैं:

सतह पर लगभग किसी भी बिंदु (अर्थात शुद्ध स्थिति) में ध्रुवों को छोड़कर कोणों के संदर्भ में एक अद्वितीय प्रतिनिधित्व है। जैसे पृथ्वी पर दक्षिणी ध्रुव के लिए कोई सुस्पष्ट देशांतर (कोई देशांतर समान कार्य करता है) है, वैसे ही$|1 \rangle$ किसी भी चरण में बताएं $\phi$एक ही बात का मतलब है। "अक्षांश"$\theta$ यहाँ है $\pi$, कि समीकरण में प्लग करें:

$$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$$ $$= 0 + e^{i \phi} |1 \rangle$$

यदि आप यूलर की पहचान से परिचित हैं, तो आप शायद पहचान लेंगे $e^{i \phi}$जटिल विमान में एक रोटेशन के रूप में। विशेष रूप से, जब से$Z$ के लिए एक रोटेशन है $\phi = \pi$, हम प्रसिद्ध हो $e^{i \pi} = -1$, अंत में पहुंचने पर $|1 \rangle = - |1 \rangle$.

Comments

This is wrong. Writing $|1\rangle=-|1\rangle$ is misleading: these are equivalent states in that they only differ by a global phase, but this doesn't mean that the state vectors are the same. You get that result because you are assuming there to be a bijection between state vectors and points on the Bloch sphere, which is not the case. The bijection stands between points on the Bloch sphere and states described as density matrices

— glS

@glS Thanks, the $1=-1$ that follows from that did seem fishy. Does it make sense to improve that answer from your perspective, or is it hopelessly wrong?

— Norrius

that is your call =). I think the proper answer is the one given by DaftWullie (I believe the asker had a similar misconception as the one in your answer). I don't see much left to be said about this question

— glS