गेट मॉडल द्वारा क्वांटम एनीलिंग का वर्णन क्यों नहीं किया जा सकता है?

यह एक सवाल है जो मुझे इस सवाल के आधार पर पूछने के लिए प्रेरित किया गया था , जो नोट करता है कि क्वांटम एनीलिंग सामान्य सर्किट मॉडल की तुलना में गणना के लिए एक पूरी तरह से अलग मॉडल है। मैंने यह पहले सुना है, और यह मेरी समझ है कि गेट-मॉडल क्वांटम-एनीलिंग पर लागू नहीं होता है, लेकिन मैं कभी नहीं समझ पाया कि ऐसा क्यों है, या उन गणनाओं को पार्स कैसे किया जाए जो एनीलर कर सकता है। जैसा कि मैं कई वार्ताओं (डी-वे खुद से!) से समझता हूं कि यह तथ्य कि एनीलर्स इसमें एक विशिष्ट हैमिल्टन नाटकों तक ही सीमित हैं।

d-wave models annealing

— एमिली टाइहर्स्ट
स्रोत

जवाबों:

इस तरह के एक डी-वेव मशीन के रूप में एक क्वांटम annealer, आइसिंग मॉडल की एक भौतिक प्रतिनिधित्व है और इस तरह के रूप में एक 'समस्या' फार्म के Hamiltonian है

{एच}_{पी} = Σ_{जम्मू = 1}^{n} ज_{j} σ_{j}^{z} + \underset{मैं, j}{Σ} {जम्मू}_{मैं j} σ_{मैं}^{z} σ_{j}^{z} ।

$H_P = \sum_{J=1}^nh_j\sigma_j^z + \sum_{i, j}J_{ij}\sigma_i^z\sigma_j^z.$

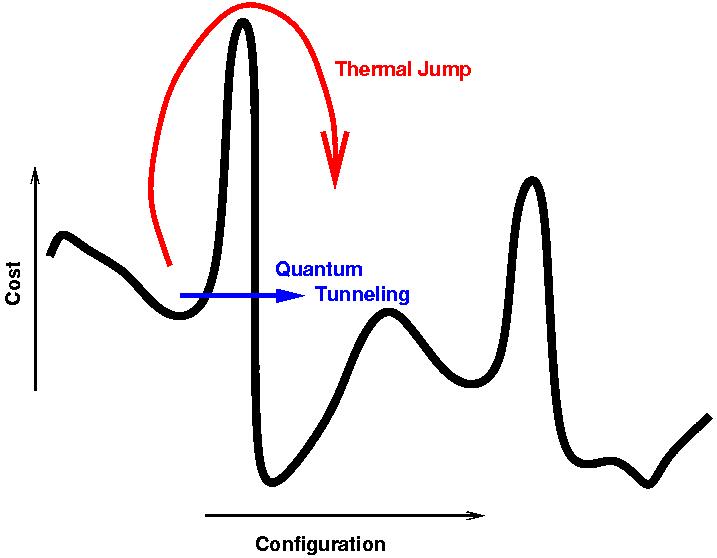
अनिवार्य रूप से, हल की जाने वाली समस्या को उपरोक्त हैमिल्टन के लिए मैप किया जाता है। Hamiltonian साथ प्रणाली शुरू होता है और annealing पैरामीटर, प्रारंभिक Hamiltonian मैप करने के लिए प्रयोग किया जाता है समस्या Hamiltonian को का उपयोग कर । $H_I = \sum_{J=1}^nh'_j\sigma_j^x$ $s$ $H_I$ $H_P$ $H\left(s\right) = \left(1-s\right)H_I + sH_P$

जैसा कि यह एक वार्षिकी है, प्रक्रिया को धीरे-धीरे पर्याप्त रूप से सिस्टम की जमीनी स्थिति के पास रहने के लिए किया जाता है जबकि हैमिल्टनियन समस्या से अलग है, नट के उत्तर में वर्णित के रूप में जमीन की स्थिति के पास रहने के लिए सुरंग का उपयोग कर रहा है ।

अब, इसका उपयोग गेट मॉडल QC का वर्णन करने के लिए क्यों नहीं किया जा सकता है? ऊपर एक द्विघात असंबंधित बाइनरी ऑप्टिमाइज़ेशन (क्यूयूबीओ) समस्या है, जो एनपी-हार्ड है ... वास्तव में, यहां एक लेख ईपींग मॉडल के लिए एनपी समस्याओं की एक संख्या का मानचित्रण है । एनपी में किसी भी समस्या को बहुपद समय में किसी भी एनपी-हार्ड समस्या के लिए मैप किया जा सकता है और पूर्णांक कारक वास्तव में एक एनपी समस्या है।

खैर, तापमान गैर-शून्य है, इसलिए यह पूरे एनील में जमीनी स्थिति में नहीं है और परिणामस्वरूप, समाधान अभी भी लगभग एक ही है। या, अलग-अलग शब्दों में, विफलता की संभावना आधे से अधिक है (यह कहीं भी सफल होने की संभावना के आस-पास नहीं है कि एक सार्वभौमिक क्यूसी 'सभ्य' के साथ तुलना में क्या करता है - मैंने जिन ग्राफों को देखा है, उन्हें देखते हुए सफलता की संभावना अधिक है। वर्तमान मशीन लगभग और यह केवल बढ़ते आकार के साथ खराब हो जाएगा), और एनील एल्गोरिथ्म बाध्य त्रुटि नहीं है। बिलकुल। इस प्रकार, यह जानने का कोई तरीका नहीं है कि आपको पूर्णांक कारक के साथ सही समाधान मिला है या नहीं। $0.2\%$

यह (सिद्धांत रूप में) सटीक परिणाम के बहुत करीब पहुंच जाता है, बहुत जल्दी, लेकिन यह किसी भी चीज के लिए मदद नहीं करता है, जहां सटीक परिणाम की आवश्यकता होती है क्योंकि 'लगभग सही' से 'सही' तक जाना अभी भी एक अत्यंत कठिन है ( आम तौर पर अभी भी सामान्य रूप से एनपी, जब मूल समस्या एनपी में है) समस्या इस मामले में, क्योंकि जो पैरामीटर हैं / 'लगभग सही' समाधान देते हैं, जरूरी नहीं कि पैरामीटर के पास कहीं भी वितरित होने जा रहे हैं / दे। सही समाधान।

स्पष्टीकरण के लिए संपादित करें: इसका मतलब यह है कि क्वांटम एनिलर (क्यूए) अभी भी एनपी समस्याओं को हल करने के लिए घातीय समय (यद्यपि एक तेज घातीय समय) लेता है, जैसे पूर्णांक कारक, जहां एक सार्वभौमिक QC एक घातीय गति देता है और वही हल कर सकता है पाली समय में समस्या। इसका तात्पर्य यह है कि एक क्यूए पाली समय में एक सार्वभौमिक क्यूसी का अनुकरण नहीं कर सकता है (अन्यथा यह पाली समय में समस्याओं को हल कर सकता है जो यह नहीं कर सकता है)। जैसा कि टिप्पणियों में बताया गया है, यह कहने के समान नहीं है कि एक क्यूए अन्य समस्याओं जैसे डेटाबेस खोज में समान स्पीडअप नहीं दे सकता है।

— Mithrandir24601
स्रोत

अगर मैं सही तरीके से समझूं, तो आप मूल रूप से कह रहे हैं कि एक क्वांटम एनीलर क्वांटम सर्किट का वर्णन नहीं कर सकता है क्योंकि एक मनमानी हैमिल्टन की न्यूनतम खोजने की समस्या एनपी-हार्ड है। मैं इस निहितार्थ को नहीं समझता। क्वांटम सर्किट का अनुकरण करना भी सामान्य रूप से अनुकरण करने के लिए सामान्य रूप से कठिन है (उदाहरण के लिए 1610.01808 देखें )

— glS

इसके अलावा, क्वांटम सर्किट के रूप में व्यक्त एल्गोरिदम के माध्यम से हल करने योग्य कुछ समस्याओं को क्वांटम एनीलिंग के माध्यम से भी हल किया जा सकता है। एक उल्लेखनीय उदाहरण डेटाबेस खोज है (देखें उदाहरण 1006.1696 का अनुभाग II )। इसका मतलब है कि कुछ अर्थों में एक कर सकते हैं कुछ परिस्थितियों में एक क्ष annealing समस्या में aq सर्किट मैप करें। क्या यह आपके तीसरे पैराग्राफ को भी अमान्य नहीं करता है (विशेष रूप से, यह दावा कि यह [गेट मॉडल QC का वर्णन करने के लिए उपयोग नहीं किया जा सकता है )

— glS

@glS नहीं, बिलकुल नहीं - यह अभी भी एक NP-hard समस्या के min (अपनी दूसरी टिप्पणी में कागज के अनुसार) खोजने के लिए घातांक समय लेता है, इसलिए पी (जैसे डेटाबेस सर्च) में समस्याएं होने पर जहां स्पीडअप हो सकता है सार्वभौमिक क्यूसी के साथ मेल खाने में सक्षम होना, एक एनपी समस्या को हल करना अभी भी सीमित समय के भीतर होने के लिए घातीय समय लगता है, जहां एक सार्वभौमिक क्यूसी पाली समय में एक ही समस्या को हल करने में सक्षम हो सकता है, जैसे पूर्णांक कारक। क्यूए ऐसा नहीं कर सकते हैं, एक गुणवत्ता आश्वासन पाली समय में एक सार्वभौमिक QC नहीं दिखाई जा सकतीं

— Mithrandir24601

ठीक है, लेकिन यह वह नहीं है जो आप उत्तर में कह रहे हैं (या कम से कम, स्पष्ट रूप से नहीं)। उत्तर से ऐसा लगता है कि आप कह रहे हैं कि क्यूए का उपयोग कभी भी गेट मॉडल QC के माध्यम से हल की गई समस्या को हल करने के लिए नहीं किया जा सकता है। यह कह रही है कि क्यूए कुशलता से एक एनपी कठिन समस्या (जो हल नहीं कर सकता से बहुत अलग है हो सकता है कभी कभी एक लंबी सर्किट द्वारा हल किया जा ... हालांकि मुझे नहीं लगता कि यह साबित हो चुका है, के रूप में हम नहीं जानते कि क्या फैक्टरिंग वास्तव में है एनपी-हार्ड, और अधिकांश अन्य समस्याएं जिनमें एक क्वांटम लाभ दिखाया गया है, निर्णय समस्याएं नहीं हैं, मेरे ज्ञान के लिए)।

— glS

मैंने एक ऐसा संपादन किया है जो आशा करता है कि चीजों को स्पष्ट करेगा। यह ज्ञात नहीं है कि पी = एनपी या नहीं, यकीन है, लेकिन यह अभी भी क्यूसी का एक विशिष्ट उदाहरण है तेजी से तेजी से किया जा रहा है, वर्तमान ज्ञान के अनुसार

— मिथ्रंदिर 24601

एनॉलिंग की एक एनालॉग रणनीति के अधिक।

जिस्ट यह है कि आपके पास कुछ अजीब फ़ंक्शन हैं जिन्हें आप अनुकूलित करना चाहते हैं। तो, आप इसके चारों ओर उछाल। सबसे पहले, " तापमान " बहुत अधिक है, जैसे कि चयनित बिंदु बहुत अधिक उछल सकता है। फिर जैसे ही एल्गोरिथ्म " ठंडा " होता है , तापमान नीचे चला जाता है, और शेख़ी कम आक्रामक हो जाती है।

अंततः, यह एक स्थानीय ऑप्टिमा पर बस जाता है जो आदर्श रूप से वैश्विक ऑप्टिमा की तरह अनुकूल है।

यहाँ नकली एनीलिंग (गैर-क्वांटम) के लिए एक एनीमेशन है :

लेकिन, यह क्वांटम एनीलिंग के लिए बहुत ही अवधारणा है :

इसके विपरीत, गेट-लॉजिक एनालॉग की तुलना में कहीं अधिक डिजिटल है। यह अव्यवस्थित उछल-कूद के बाद केवल एक परिणाम खोजने के बजाय qubits और तार्किक संचालन से संबंधित है।

— नेट
स्रोत

धन्यवाद, यह मेरे लिए कुछ सीमाओं को स्पष्ट करता है। क्या आप किसी भी समस्या के बारे में जानते हैं जो एक एनीलिंग समस्या के रूप में पुनःप्रकाशित करने के लिए संभव नहीं है (मुझे पता है कि विकिपीडिया ने कहा कि शोर का एल्गोरिथ्म संभव नहीं था क्योंकि यह "पहाड़ी चढ़ाई" समस्या है, लेकिन अगर आप उस की बारीकियों के बारे में अधिक जानते हैं, तो मैं उन्हें सुनना अच्छा लगेगा :)

— एमिली टाइहर्स्ट

@EmilyTyhurst तकनीकी रूप से, किसी भी समस्या को पहाड़ी पर चढ़ने वाले शब्दों में वर्णित किया जा सकता है। यह एक सवाल है कि हिल-क्लाइम्बिंग फॉर्मेट में वर्णित समस्या का कितना अच्छा व्यवहार किया जाता है। समस्याएं जो इसे अच्छी तरह से फिट नहीं करती हैं वे अविश्वसनीय रूप से बदसूरत हो सकती हैं। पूरी तरह से गैर-उत्तल समस्याओं के लिए, पहाड़ी पर चढ़ना, सबसे अच्छा, मूल रूप से एक जानवर-बल खोज होगा।

— नेट

@EmilyTyhurst Hah ऑप्स, विपरीत दिशा में आपकी टिप्पणी को गलत ठहराता है। xD लेकिन, हाँ, आप एक क्वांटम कंप्यूटर पर सिम्युलेटेड एनाउलिंग कर सकते हैं जैसे आप इसे क्लासिक कंप्यूटर पर कर सकते हैं। फिर, मुझे लगता है कि हम इसे " क्वांटम एनालिंग " कहते हैं या नहीं, यह शब्दार्थ का विषय है।

— नेट

@EmilyTyhurst हाँ, वे निश्चित रूप से सभी अंतर-परिवर्तनीय हैं। मेरा मतलब है, यह ट्यूरिंग पूर्णता की अवधारणा की तरह है - अगर हमारे पास किसी भी प्रकार का पूर्ण तर्क है, तो हम इसके बारे में और कुछ भी निर्माण कर सकते हैं।

— नट

क्वांटम एनीलिंग का एक महत्वपूर्ण बिंदु यह है कि हैमिल्टन को अदभुत रूप से बदलना ताकि राज्य हर समय (बदलते) हैमिल्टन की जमीनी स्थिति बना रहे, और आप अंतिम हैमिल्टन के जीएस के साथ समाप्त हो गए, जो कि प्रोटोकॉल का लक्ष्य है । यह आपके द्वारा यहां वर्णित "कूद" के साथ कैसे संबंधित है? यह पत्र ( 1006.1696 ) इस संबंध में रुचि का हो सकता है (विशेष रूप से, पहले पृष्ठ के दूसरे स्तंभ का अंतिम भाग)।

— glS