इस सवाल पर कि "प्रतिबाधा क्या है," मैं ध्यान दूंगा कि प्रतिबाधा सामान्य रूप से भौतिकी की एक व्यापक अवधारणा है, जिसमें से विद्युत प्रतिबाधा केवल एक उदाहरण है।
इसका क्या अर्थ है और यह कैसे काम करता है, इसकी समझ पाने के लिए, इसके बजाय यांत्रिक प्रतिबाधा पर विचार करना अक्सर आसान होता है। फर्श पर एक भारी सोफे को (स्लाइड) धकेलने की कोशिश करने के बारे में सोचें।
आप एक निश्चित मात्रा में बल लागू करते हैं, और सोफे एक निश्चित वेग पर स्लाइड करता है, इस पर निर्भर करता है कि आप कितना कठिन धक्का देते हैं, सोफे का वजन, फर्श की सतह का प्रकार, पैर का प्रकार जो सोफे पर है, और इसी तरह। इस स्थिति के लिए, एक यांत्रिक प्रतिबाधा को परिभाषित करना संभव है जो कि आपको कितना कठिन धक्का देता है और सोफे कितनी तेजी से जाता है।
यह वास्तव में एक डीसी इलेक्ट्रिकल सर्किट की तरह बहुत कुछ है, जहां आप एक सर्किट में एक निश्चित मात्रा में वोल्टेज लागू करते हैं, और इसके माध्यम से एक निश्चित संगत दर पर वर्तमान प्रवाह होता है।
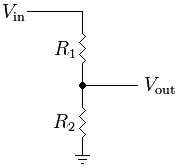
सोफे और सर्किट दोनों के मामले के लिए, आपके इनपुट की प्रतिक्रिया सरल और काफी रैखिक हो सकती है: एक अवरोधक जो ओहम के नियम का पालन करता है, जहां इसका विद्युत प्रतिबाधा प्रतिरोध है, और सोफे में घर्षण स्लाइडर हो सकता है जो इसे अनुमति देता है अपने बल के आनुपातिक वेग के साथ चलना
सर्किट और मैकेनिकल सिस्टम भी nonlinear हो सकते हैं। यदि आपके सर्किट में एक डायोड के साथ श्रृंखला में एक रोकनेवाला में रखा गया एक चर वोल्टेज होता है, तो जब तक आप डायोड के आगे वोल्टेज से अधिक नहीं होंगे, तब तक शून्य शून्य के पास होगा, जिस बिंदु पर ओम के अनुसार रोकनेवाला के माध्यम से प्रवाह शुरू हो जाएगा। कानून। इसी तरह, फर्श पर बैठे एक सोफे पर आमतौर पर कुछ हद तक स्थिर घर्षण होता है: जब तक आप प्रारंभिक बल की एक निश्चित मात्रा के साथ धक्का नहीं देते तब तक यह हिलना शुरू नहीं होगा। न तो यांत्रिक और न ही विद्युत प्रणाली में एक भी रैखिक प्रतिबाधा है जिसे परिभाषित किया जा सकता है। बल्कि, जो सबसे अच्छा आप कर सकते हैं वह है अलग-अलग परिस्थितियों में बाधाओं को अलग-अलग परिभाषित करना। (वास्तविक दुनिया इस तरह बहुत अधिक है।)
यहां तक कि जब चीजें बहुत स्पष्ट और रैखिक होती हैं, तो यह ध्यान रखना महत्वपूर्ण है कि प्रतिबाधा सिर्फ एक अनुपात का वर्णन करती है - यह सिस्टम की सीमाओं का वर्णन नहीं करती है, और यह "बुरा" नहीं है। आप निश्चित रूप से अधिक वर्तमान / वेग प्राप्त कर सकते हैं जैसा कि आप चाहते हैं (एक आदर्श प्रणाली में) अधिक वोल्टेज जोड़कर / कठिन धक्का देकर।
मैकेनिकल सिस्टम भी एसी प्रतिबाधा के लिए एक बहुत अच्छा एहसास दे सकता है। कल्पना कीजिए कि आप एक साइकिल की सवारी कर रहे हैं। पैडल के प्रत्येक आधे-चक्र के साथ, आप बाएं को धक्का देते हैं, दाएं को धक्का देते हैं। आप सिर्फ एक पैर और एक पैर की अंगुली-क्लिप के साथ पेडलिंग करने की कल्पना कर सकते हैं, जैसे कि आप अपने पैडल के हर चक्र के साथ धक्का और खींचते हैं। यह एक सर्किट में एक एसी वोल्टेज लागू करने जैसा बहुत कुछ है: आप किसी दिए गए आवृत्ति पर, बारी-बारी से चक्रीय रूप से धक्का देते हैं और खींचते हैं।
यदि आवृत्ति काफी धीमी है - जैसे जब आप बाइक पर रुकते हैं, तो पैडल पर नीचे धकेलने की समस्या बस एक "डीसी" समस्या है, जैसे कि सोफे को धक्का देना। जब आप गति करते हैं, हालांकि, चीजें अलग तरह से कार्य कर सकती हैं।
अब, मान लीजिए कि आप एक निश्चित गति से बाइक चला रहे हैं, और आपकी बाइक कम, मध्यम और हाय गियर अनुपात के साथ एक तीन गति है। मध्यम प्राकृतिक लगता है, हाय गियर किसी भी अंतर को बनाने के लिए पर्याप्त बल लागू करना मुश्किल है, और कम गियर में, आप पहियों को किसी भी ऊर्जा को स्थानांतरित किए बिना पैडल को स्पिन करते हैं। यह प्रतिबाधा मिलान का विषय है , जहां आप केवल पहियों को प्रभावी ढंग से स्थानांतरित कर सकते हैं जब वे आपके पैर की एक निश्चित मात्रा में भौतिक प्रतिरोध प्रस्तुत करते हैं - बहुत अधिक नहीं, बहुत कम नहीं। इसी विद्युत घटना के रूप में अच्छी तरह से बहुत आम है; आपको पॉइंट ए से पॉइंट बी तक आरएफ पावर को प्रभावी ढंग से प्रसारित करने के लिए प्रतिबाधा मिलान लाइनों की आवश्यकता होती है, और किसी भी समय जब आप दो ट्रांसमिशन लाइनों को एक साथ जोड़ते हैं, तो इंटरफ़ेस में कुछ नुकसान होगा।
आपके पैरों को पैडल जो प्रतिरोध प्रदान करता है, वह आपके द्वारा दबाए जाने के लिए कितना आनुपातिक है, जो इसे एक साधारण प्रतिरोध के सबसे निकट से संबंधित करता है - विशेष रूप से कम गति पर। एसी सर्किट में भी, एक रोकनेवाला एक प्रतिरोधक (एक निश्चित बिंदु तक) की तरह व्यवहार करता है।
हालांकि, एक रोकनेवाला के विपरीत, एक साइकिल का प्रतिबाधा आवृत्ति पर निर्भर है। मान लीजिए कि आपने अपनी बाइक को एक स्टॉप से शुरू करके उच्च गियर में रखा है। इसे शुरू करना बहुत कठिन हो सकता है । लेकिन, एक बार जब आप शुरू हो जाते हैं, तो पेडल द्वारा प्रस्तुत प्रतिबाधा नीचे चली जाती है क्योंकि आप तेजी से जा रहे हैं, और एक बार जब आप बहुत तेजी से जा रहे हैं, तो आप पा सकते हैं कि पैडल आपके पैरों से शक्ति को अवशोषित करने के लिए बहुत कम प्रतिबाधा प्रस्तुत करते हैं। तो वास्तव में एक आवृत्ति-निर्भर प्रतिबाधा (एक प्रतिक्रिया ) है जो उच्च बाहर शुरू होती है और उच्च आवृत्ति के लिए सिर के रूप में कम हो जाती है।
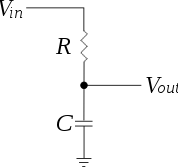
यह एक संधारित्र के व्यवहार की तरह है, और एक साइकिल के यांत्रिक प्रतिबाधा के लिए काफी अच्छा मॉडल एक संधारित्र के साथ समानांतर में एक अवरोधक होगा।
डीसी (शून्य वेग) पर, आप बस अपने प्रतिबाधा के रूप में उच्च, निरंतर प्रतिरोध देखते हैं। जैसे ही पेडलिंग आवृत्ति बढ़ती है, संधारित्र प्रतिबाधा अवरोधक की तुलना में कम हो जाता है, और वर्तमान को इस तरह से प्रवाह करने की अनुमति देता है।
बेशक, विभिन्न अन्य बिजली के घटकों और उनके यांत्रिक उपग्रहों ** हैं, लेकिन इस चर्चा से आपको सामान्य अवधारणा पर कुछ प्रारंभिक अंतर्ज्ञान देना चाहिए ताकि आप समय पर लगने वाले गणितीय पहलुओं के बारे में जान सकें। बहुत सार विषय की तरह।
* अचार के लिए एक शब्द: ओम का नियम एक वास्तविक उपकरण के लिए कभी भी सटीक नहीं होता है, और वास्तविक दुनिया के घर्षण बल कभी भी वेग को बल के समानुपाती नहीं देते हैं। हालांकि, "काफी रैखिक" आसान है। मैं यहां सभी शैक्षिक और सामान होने की कोशिश कर रहा हूं। कट मी सम स्लैक।
** उदाहरण के लिए, एक प्रारंभ करनेवाला आपके पहिया पर एक स्प्रिंग-लोडेड रोलर की तरह होता है जो उच्च आवृत्ति पर आते ही ड्रैग जोड़ता है)