क्या मर्ज सॉर्ट में "डिवाइड" कदम से बचा जा सकता है?

Question

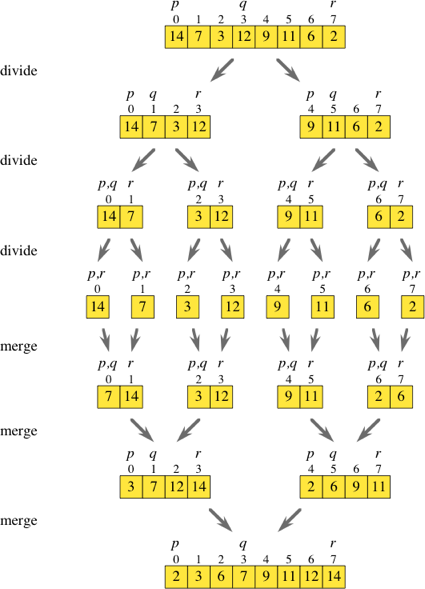
तो मर्ज सॉर्ट एक विभाजित और एल्गोरिथ्म को जीत है। जब मैं उपरोक्त आरेख को देख रहा था, तो मैं सोच रहा था कि क्या मूल रूप से सभी विभाजन चरणों को बायपास करना संभव है।

यदि आप दो से कूदते समय मूल सरणी पर पुनरावृत्त होते हैं, तो आप तत्वों को इंडेक्स i और i + 1 पर प्राप्त कर सकते हैं और उन्हें अपने स्वयं के क्रमबद्ध सरणियों में डाल सकते हैं। एक बार जब आप इन सभी उप-सरणियों ([7,14], [3,12], [9,11] और [2,6] जैसा कि आरेख में दिखाया गया है), आप बस सामान्य मर्ज दिनचर्या के साथ आगे बढ़ सकते हैं एक क्रमबद्ध सरणी।

क्या सरणी के माध्यम से पुनरावृत्ति हो रही है और तुरंत आवश्यक उप-सरणियों को कम करने से उनकी संपूर्णता में विभाजन के चरणों का प्रदर्शन करने की तुलना में कम कुशल है?

Comments

संबंधित: cs.stackexchange.com/questions/77075/...

— उमर

Answer 1

एल्गोरिथ्म के वैचारिक विवरण और इसके कार्यान्वयन के बीच अंतर से भ्रम पैदा होता है ।

तार्किक रूप से मर्ज सॉर्ट को सरणी को छोटे सरणियों में विभाजित करने के रूप में वर्णित किया जाता है, और फिर उन्हें वापस एक साथ विलय कर दिया जाता है। हालाँकि, "सरणी को विभाजित करना" "स्मृति में एक पूरी तरह से नया सरणी बनाने" का अर्थ नहीं है, या ऐसा कुछ भी - यह कोड में हो सकता है

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

अर्थात कोई वास्तविक कार्य नहीं होता है, और "विभाजन" विशुद्ध रूप से वैचारिक है। तो आप जो सुझाव देते हैं वह निश्चित रूप से काम करता है, लेकिन तार्किक रूप से आप अभी भी सरणियों को "विभाजित" कर रहे हैं - ऐसा करने के लिए आपको कंप्यूटर से किसी भी काम की आवश्यकता नहीं है :-)

Comments

व्यक्तिगत रूप से मुझे वास्तव में नीचे वाला मर्ज सॉर्ट पसंद है क्योंकि यह इस तरह से लागू करना सरल है जिससे आप प्रत्येक रिकर्सन स्तर पर एक अस्थायी बफर को आवंटित करने से बच सकते हैं। इसके बजाय आप एक बार एक बफर आवंटित करें और उनके बीच पिंग-पोंग करें।

— शाफ़्ट फ्रेक

यह - डिवाइड कम्प्यूटेशनल रूप से एक नो-ऑप है ... प्लस ओपी सुझाव केवल एकल तत्व सरणियों के विलय के बराबर है, और 2 डी चरण से मर्ज का उपयोग करना शुरू कर रहा है, जो बेमानी लगता है, क्योंकि मूल मर्ज बस के रूप में भी काम करता है। इसका अनुकूलन करने का कोई मतलब नहीं है। यह केवल निरर्थक अवधारणाओं और तर्क का परिचय देता है।

— luk32

@ratchetfreak: मैं भी इसे प्यार करता हूँ, लेकिन दुख की बात है कि यह टॉप-डाउन (कम से कम मुझे पता है संस्करण) के बराबर नहीं है। यह विलय को अलग तरीके से करेगा, मूल रूप से अगले पावर-ऑफ -2 सरणी लंबाई तक, जो मुझे लगता है कि थोड़ा धीमा भी हो सकता है। क्या आप एक नीचे-ऊपर संस्करण के बारे में जानते हैं जो एक समान लागत का भुगतान किए बिना सटीक रूप से विलय करता है?

— user541686

@ मेहरदाद एकमात्र वास्तविक मुद्दा वह छोटी पूंछ है जिसे विलय करने की आवश्यकता है। सबसे खराब स्थिति में इसका मतलब है कि लंबाई की सरणियों के लिए किसी एक आइटम में विलय करने के लिए एक और पास 1<<n+1। हालांकि मुझे यकीन है कि आप चीजों को समायोजित कर सकते हैं इसलिए बहुत छोटी पूंछ कम पास में विलय हो जाती है।

— शाफ़्ट

@psmears "आपको बस ऐसा करने के लिए कंप्यूटर से किसी भी काम की आवश्यकता नहीं है" - इसलिए मैं अनुमान लगा रहा हूं कि कुछ पुनरावर्ती डिवाइड फ़ंक्शन के n कॉल्स (उदाहरण आरेख में 7 कॉल) की प्रदर्शन लागत मूल रूप से नगण्य है?

— जिमी_रस्टल

Answer 2

मुझे लगता है कि आपका मतलब क्या है नीचे-ऊपर कार्यान्वयन । नीचे के कार्यान्वयन में आप एकल सेल तत्वों से शुरू करते हैं जो तत्वों को बड़े क्रमबद्ध सूचियों / सरणियों में विलय करके ऊपर की ओर बढ़ते हैं। मध्य सरणी, यानी एक-तत्व सरणियों से शुरू करके ऊपर अपने आंकड़े में तीर को उल्टा करें।

इसके अलावा, आप सरणियों को विभाजित करके मर्ज सॉर्ट को ऑप्टिमाइज़ करना चाह सकते हैं जब तक कि वे कुछ स्थिर आकार तक नहीं पहुंच जाते हैं, जिसके बाद आप उदाहरण के सॉर्टिंग सॉर्ट का उपयोग करके उन्हें बस सॉर्ट करते हैं।

अन्यथा, विभाजन विभाजन के बिना छांटना संभव नहीं है। वास्तव में मर्ज के प्रकार को विभाजित किया जा रहा है और उप-प्रकारों को विभाजित कर रहा है, अर्थात, विभाजन और जीत।