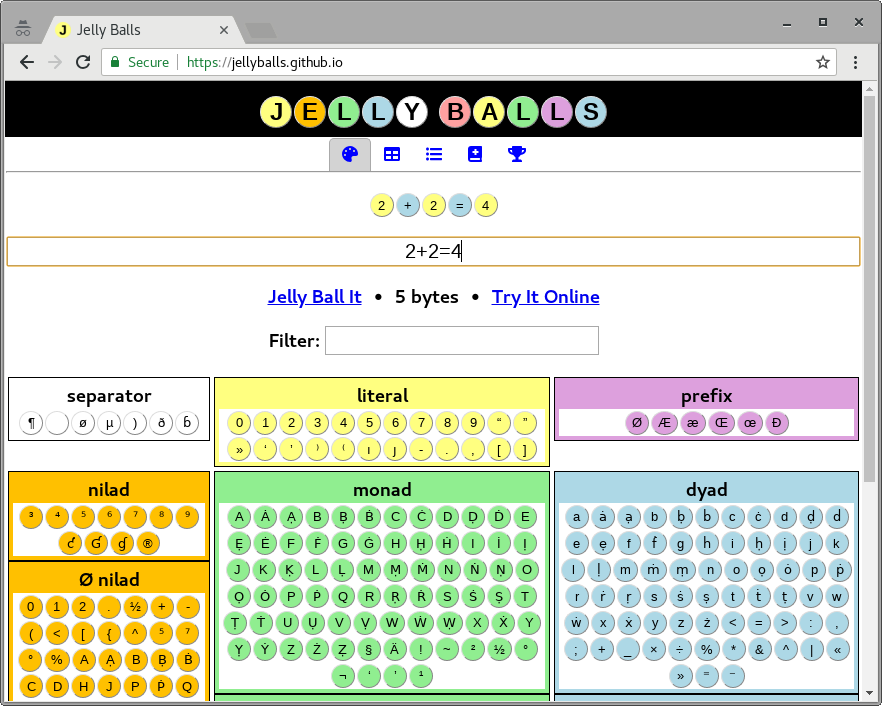
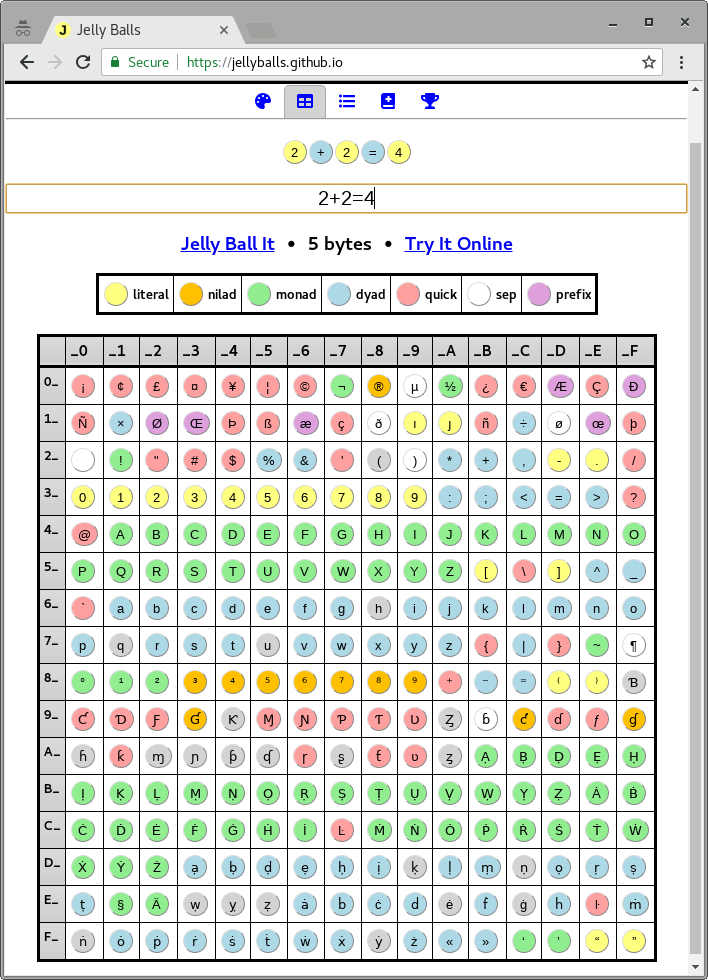
सूची कमांड और शाब्दिक
आप में से कई का उपयोग करने का प्रयास करते हैं गैर vectorizing सूची आदेशों एक पर शाब्दिक n या एक शाब्दिक की सूची z , सूची आदेश पहले किसी प्रकार की एक सूची के लिए परिवर्तित कर देंगे और फिर उस सूची पर आदेश बाहर ले जाने के।
ये कमांड jelly.pyiterable फ़ंक्शन को कॉल का उपयोग करते हुए दिखाई देते हैं ।
def iterable(argument, make_copy = False, make_digits = False, make_range = False):
the_type = type(argument)
if the_type == list:
return copy.deepcopy(argument) if make_copy else argument
if the_type != str and make_digits:
return to_base(argument, 10)
if the_type != str and make_range:
return list(range(1, int(argument) + 1))
return [argument]
यहाँ कुछ अपूर्ण सूची दी गई है कि उन सूची कमांड क्या करेंगे।
एक सूची में लपेटता है
iterableकिसी सूची में तर्क को लपेटने के लिए सबसे सरल रिटर्न , और फ़ंक्शन द्वारा संसाधित किए जाने वाले रिटर्न। ऐसा तब होता है जब तर्क पहले से ही एक सूची नहीं है, एक स्ट्रिंग है, और iterableतर्क अन्य तरीकों के लिए कॉल नहीं करते हैं।
-------------------------------------------------------------------------------
| Command | Description | Process | Effect |
-------------------------------------------------------------------------------
| F | Flattens a list | 4953F -> [4953]F -> [4953] | Same as W |
-------------------------------------------------------------------------------
| G | Format a list | 4953G -> [4953]G -> [4953] | Same as W |
| | as a grid | | |
-------------------------------------------------------------------------------
| I | Increments | 4953I -> [4953]I -> <nothing> | Empty list |
-------------------------------------------------------------------------------
| S | Sums a list | 4953S -> [4953]S -> 4953 | Same as ¹ |
-------------------------------------------------------------------------------
| Ṭ | Boolean array, | 4Ṭ -> [4]Ṭ -> [0, 0, 0, 1] | n-1 zeroes, |
| | 1s at indices | | 1 at end |
-------------------------------------------------------------------------------
| Ụ | Sort indices by | 4Ụ -> [4]Ụ -> [1] | Yields [1] |
| | by their values | | |
-------------------------------------------------------------------------------
| Ė | Enumerate list | 4Ė -> [4]Ė -> [[1, 4]] | Yields [[1, n]] |
-------------------------------------------------------------------------------
| Ġ | Group indices | 4Ġ -> [4]Ġ -> [[1]] | Yields [[1]] |
| | by values | | |
-------------------------------------------------------------------------------
| Œr | Run-length | 4Œr -> [4]Œr -> [[4, 1]] | Yields [[n, 1]] |
| | encode a list | | |
-------------------------------------------------------------------------------
बेस 10 में कन्वर्ट करें
यहां फ़ंक्शन iterableएक संख्या को अपने अंकों की सूची में धर्मान्तरित करने के लिए कहते हैं D, और फिर उन अंकों पर चलते हैं।
-------------------------------------------------------------------------
| Command | Description | Process | Effect |
-------------------------------------------------------------------------
| Q | Unique elements | 299Q -> [2, 9, 9]Q -> [2, 9] | Unique |
| | ordered by | | digits |
| | appearance | | of n |
-------------------------------------------------------------------------
| Ṛ | Non-vectorized | 4953Ṣ -> [4, 9, 5, 3]Ṛ | Reverses D |
| | reverse | -> [3, 5, 4, 9] | |
-------------------------------------------------------------------------
| Ṣ | Sort a list | 4953Ṣ -> [4, 9, 5, 3]Ṣ | Sorts D |
| | | -> [3, 4, 5, 9] | |
-------------------------------------------------------------------------
श्रेणी के साथ सूची में परिवर्तित करें
यहां फ़ंक्शन एक संख्या को श्रेणी में परिवर्तित करते हैं R = [1 ... n], और फिर उस सीमा पर चलते हैं।
-----------------------------------------------------------------------------------------
| Command | Description | Process | Effect |
-----------------------------------------------------------------------------------------
| X | Random element | 4R -> [1 ... 4]X -> 2 | Random element |
| | | | of R |
| | | | |
-----------------------------------------------------------------------------------------
| Ḋ | Dequeue from list | 4R -> [1 ... 4]Ḋ -> [2, 3, 4] | Range [2 ... n] |
-----------------------------------------------------------------------------------------
| Ṗ | Pop from list | 4Ṗ -> [1 ... 4]Ṗ -> [1, 2, 3] | Range [1 ... n-1] |
-----------------------------------------------------------------------------------------
| Ẇ | Sublists of list | 4Ẇ -> [1 ... 4]Ẇ | All sublists of R |
| | | -> [[1], [2], [3], [4], [1, 2], | |
| | | [2, 3], [3, 4], [1, 2, 3], | |
| | | [2, 3, 4], [1, 2, 3, 4]] | |
-----------------------------------------------------------------------------------------
| Ẋ | Shuffle list | 4Ẋ -> [1 ... 4]Ẋ -> [2, 1, 3, 4] | Shuffles R |
-----------------------------------------------------------------------------------------
| Œ! | All permutations | 3Œ! -> [1, 2, 3]Œ! | All permutations |
| | of a list | -> [[1, 2, 3], [1, 3, 2], | of R |
| | | [2, 1, 3], [2, 3, 1], | |
| | | [3, 1, 2], [3, 2, 1]] | |
-----------------------------------------------------------------------------------------
| ŒḄ | Non-vectorized | 4ŒḄ -> [1 ... 4]ŒḄ | Bounces R |
| | bounce, | -> [1, 2, 3, 4, 3, 2, 1] | |
| | z[:-1] + z[::-1] | | |
-----------------------------------------------------------------------------------------
| Œc | Unordered pairs | 4Œc -> [1 ... 4]Œc | Unordered pairs |
| | of a list | -> [[1, 2], [1, 3], [1, 4], [2, 3], | of R |
| | | [2, 4], [3, 4]] | |
-----------------------------------------------------------------------------------------
| Œċ | Unordered pairs | 4Œċ -> [1 ... 4]Œċ | Unordered pairs |
| | with replacement | -> [[1, 1], [1, 2], [1, 3], [1, 4], | with replacement |
| | of a list | [2, 2], [2, 3], [2, 4], [3, 3], | of R |
| | | [3, 4], [4, 4]] | |
-----------------------------------------------------------------------------------------
| ŒP | Powerset of | 3ŒP -> [1 ... 3] | Powerset of R |
| | a list | -> ['', [1], [2], [3], [1, 2], | |
| | | [1, 3], [2, 3], [1, 2, 3]] | |
-----------------------------------------------------------------------------------------
| Œp | Cartesian | 4,2Œp -> [[1 ... 4], [1 ... 2]]Œp | Cartesian product |
| | product of z's | -> [[1, 1], [1, 2], [2, 1], [2, 2], | of [1 ... z[i]] |
| | items | [3, 1], [3, 2], [4, 1], [4, 2]] | for i in z |
-----------------------------------------------------------------------------------------