समस्या को O (बहुभुज (b)) में हल किया जा सकता है।
हम f(d, n)d दशमलव अंकों के पूर्णांक की संख्या को n से कम या उसके बराबर अंक के साथ परिभाषित करते हैं। यह देखा जा सकता है कि यह फ़ंक्शन सूत्र द्वारा दिया गया है

चलो कुछ सरल से शुरू करते हुए, इस फ़ंक्शन को प्राप्त करें।
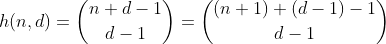
फ़ंक्शन h, d + 1 तत्वों को चुनने के तरीकों की संख्या को गिनता है, जिसमें n-1 विभिन्न तत्वों वाले बहु-सेट होते हैं। यह भी तरीकों की संख्या है n n को d डिब्बे में विभाजित करने के लिए, जो आसानी से d - 1 बाड़ n के आसपास बनाकर देखी जा सकती है और प्रत्येक अलग-अलग अनुभाग को जोड़ सकती है। N = 2, d = 3 'के लिए उदाहरण:
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
तो, h, n और d अंकों के अंक-योग वाली सभी संख्याओं को गिनता है। सिवाय इसके कि यह केवल 10 से कम n के लिए काम करता है, क्योंकि अंक 0 - 9 तक सीमित हैं। 10 - 19 मानों के लिए इसे ठीक करने के लिए, हमें उन विभाजनों की संख्या को घटाना होगा, जिनकी संख्या 9 से अधिक के साथ एक बिन है, जिसे मैं अब से ओवरफ्लो बिन कहूंगा।
निम्नलिखित तरीके से h का पुन: उपयोग करके इस शब्द की गणना की जा सकती है। हम n - 10 के विभाजन के तरीकों की संख्या की गणना करते हैं, और फिर 10 में डालने के लिए एक डिब्बे का चयन करते हैं, जिसके परिणामस्वरूप एक से अधिक बिन वाले विभाजन की संख्या होती है। परिणाम निम्नलिखित प्रारंभिक कार्य है।
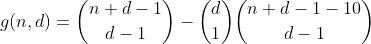
हम इस तरह से n कम या बराबर 29 के लिए जारी रखते हैं, विभाजन के सभी तरीकों की गिनती करके n - 20, फिर 2 डिब्बे का चयन करते हैं जहां हम 10 का डालते हैं, जिससे 2 ओवरफ्लो डिब्बे वाले विभाजन की संख्या की गणना होती है।
लेकिन इस बिंदु पर हमें सावधान रहना होगा, क्योंकि हमने पहले ही पिछले कार्यकाल में 2 ओवरफ्लो डिब्बे वाले विभाजन गिना। केवल इतना ही नहीं, बल्कि वास्तव में हमने उन्हें दो बार गिना। आइए एक उदाहरण का उपयोग करें और 21 के साथ विभाजन (10,0,11) को देखें। पिछले कार्यकाल में, हमने 10 को घटाया, शेष 11 के सभी विभाजन की गणना की और 10 को 3 डिब्बे में से एक में डाल दिया। लेकिन इस विशेष विभाजन को दो तरीकों में से एक में पहुँचा जा सकता है:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
चूँकि हमने पहले भाग में एक बार इन विभाजनों को भी गिना था, इसलिए 2 अतिप्रवाह बिन के साथ विभाजनों की कुल संख्या 1 - 2 = -1 है, इसलिए हमें अगला पद जोड़कर एक बार और गिनना होगा।
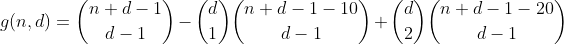
इस बारे में थोड़ा और सोचने पर, हमें जल्द ही पता चलता है कि एक विशेष संख्या में ओवरफ्लो डिब्बे की संख्या के साथ एक विभाजन को एक विशिष्ट शब्द में गिना जाता है, जिसे निम्न तालिका द्वारा व्यक्त किया जा सकता है (कॉलम i, जो शब्द i का प्रतिनिधित्व करता है, पंक्ति j विभाजन को jflown के साथ डिब्बे)।
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
हाँ, यह पास्कल त्रिकोण है। केवल हम जिस चीज में रुचि रखते हैं, वह पहली पंक्ति / कॉलम में से एक है, यानी शून्य ओवरफ्लो डिब्बे के साथ विभाजन की संख्या। और हर पंक्ति के वैकल्पिक योग के बाद से पहले 0 (जैसे 1 - 4 + 6 - 4 + 1 = 0) के बराबर है, कि कैसे हम उनसे छुटकारा पा लेते हैं और प्रायद्वीप सूत्र पर पहुंचते हैं।
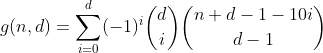
यह फ़ंक्शन सभी अंकों को गिनता है, जिसमें d अंकों के साथ n का अंक-योग होता है।
अब, अंक से योग के बारे में क्या n से कम है? हम यह दिखाने के लिए कि एक द्विपद प्लस एक आगमनात्मक तर्क के लिए एक मानक पुनरावृत्ति का उपयोग कर सकते हैं
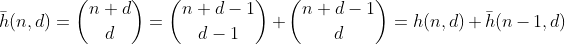
अधिकांश n पर अंक-योग के साथ विभाजन की संख्या को गिना जाता है। और इस f से g के समान ही तर्कों का उपयोग करके व्युत्पन्न किया जा सकता है।
इस सूत्र का उपयोग करते हुए, हम उदाहरण के लिए 8000 से 8999 के अंतराल में भारी संख्या की संख्या का पता लगा सकते हैं 1000 - f(3, 20), क्योंकि इस अंतराल में हजार संख्याएँ हैं, और हमें अंकों की संख्या को अंकों के योग से घटाकर 28 के बराबर या उससे कम करना होगा। एकांत में ले जाते समय कि पहला अंक पहले से 8 अंक के योग में योगदान देता है।
अधिक जटिल उदाहरण के रूप में आइए अंतराल 1234..5678 में भारी संख्या की संख्या को देखें। हम सबसे पहले १२ चरणों में १२३४ से १२४० तक जा सकते हैं। फिर हम १०४० के चरणों में १२४० से १३०० तक जाते हैं। उपरोक्त सूत्र हमें प्रत्येक ऐसे अंतराल में भारी संख्या की संख्या देता है:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
अब हम 100 के चरणों में 1300 से 2000 तक जाते हैं:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
1000 के चरणों में 2000 से 5000 तक:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
अब हमें फिर से स्टेप साइज को कम करना होगा, 100 के चरणों में 5000 से 5600 तक, 10 के चरणों में 5600 से 5670 तक और अंत में 1 के चरणों में 5670 से 5678 तक जाना होगा।
एक उदाहरण पायथन कार्यान्वयन (जो थोड़ी सी अनुकूलन और इस बीच परीक्षण प्राप्त हुआ):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
संपादित करें : कोड को एक अनुकूलित संस्करण द्वारा प्रतिस्थापित किया गया है (जो मूल कोड की तुलना में भी बदसूरत दिखता है)। जब मैं उस पर था तब कुछ कोने के मामले भी तय किए। heavy(1234, 100000000)मेरी मशीन पर लगभग एक मिलीसेकंड लगता है।
